Advances in recent technology have enabled miniaturization, low power consumption, and wireless communication, which have facilitated the acquisition of basic data (electromyography, movement, etc.) espe- cially for motion analysis in the field of sports science.

A study by Stuart and Atha (1990), which was the first to analyze postural consistency in the field of archery, attached markers on the archer's head and the elbow of the drawing arm, as well as on the bow above where the bow was held by the hand. The authors then recorded the changes in the position of those aforementioned markers with a camera when the bowstring was released, and subsequently analyzed the recorded motion. In a recent study by Ertan (2009), the muscle activation patterns of the M. flexor digitorum superficialis (MFDS) and M. extensor digitorum (MED) in the bow arm during bowstring release were measured by electromyographic (EMG) signals, and the findings were analyzed. In addition, motion analysis was conducted in a study by Horask and Heller (2011) by attaching 20 markers on the hand of the drawing arm (more specifically, the fingers, top of the hand, and wrist) and using eight infrared cameras to record the positional changes in the markers during bowstring release. In short, these studies analyzed the motion of the moment of arrow release and used cameras or EMG signals for data acquisition. Cameras have limited use in places sensitive to light, and it is cumbersome to attach markers. However, motion analysis systems combined with cameras are widely used as analysis tools, and similarly, although there are many tools that analyze EMG signals, these tools require great care with respect to the locations and methods of attaching the electrodes. Consideration must also be given to whether such systems can be easily applied to athletes, in non-laboratory settings, for data acquisition.

A study by Kian, Ghomshe and Norang (2013) also used cameras to analyze the bow arm movements. A recent study by Polak, Kulasa, VencesBrito, Castro and Fernandes (2016) that investigated motion analysis systems showed that various tools or systems are available for motion analysis in the field of sports science, and systems that utilize inertia sensors (acceleration) are quite notable in particular, resulting in a broad range of choice in motion analysis tools.

Despite this fact, a closer look at recent studies in the sports science field shows that most of the studies approached their research with traditional methods, which include using EMG signals to analyze the effects of the major upper extremity muscles on the performance out- comes in air pistol shooting (Kim, 2016), using cameras to analyze kinematic characteristics of upper and lower extremity joints in rowing athletes (Kim et al., 2016), and using a force plate to study stability in Taekwondo athletes (Hyun, Kim & Ryew, 2016).

In the present study, compact (37.6 mm x 52 mm x 18.1 mm) and lightweight (34 g) wireless inertial sensors (working range: typical 30 m, battery life: >8 hr) were attached to the body. The method for attaching the sensors involved wrapping the body with a band that was pro- vided and placing the sensor in the band pocket. The sensors were easily attached to different parts of the athlete's body and the motion (acceleration and others) during archery shooting was recorded in real time. Another point that differed from previous studies was that the present study used data of motion defined by aiming pattern during holding and aiming phases immediately prior to releasing the bowstring, lasting about 2 sec, rather than the motion of the moment of arrow release.

The present study was planned for the purpose of investigating the relationship between scores and aiming pattern defined as athlete's motion immediately before the shot. The athlete's raw motion data were acquired using the inertial sensors and the Dynamic Time Warping (DTW) algorithm was used to automatically extract the data to be analyzed, which were then used in multiple regression analysis. Based on the results of the regression analysis, the study was able to identify differences in shooting motions in four athletes, specific body parts that affected scores, and the relative importance of movement of each body part on scores. The approaches used in the present study are expected to be applicable not only in archery, but in various systems for motion analysis in the field of sports science.

1. Participants

The participants in the present study consisted of four female junior high school archery team members (age: 16, 14, 15, and 14 yr, mean = 14.75 ± 0.96 yr; height: 158 cm, 157 cm, 171 cm, and 164 cm, mean = 162.5 ± 6.45 cm; weight: 53 kg, 49 kg, 62 kg, and 52 kg, mean = 54 ± 5.60 kg; previous season's score: 59, 59, 55, and 54, mean = 56.75 ± 2.63). All participants were provided with an explanation of the study purpose and procedures prior to the experiment, after which their intent and consent to participate were obtained. The experiment was con- ducted in the archery range of the school the athletes attended.

2. Measurements

1) Attachment of 3-axis inertial sensors

The present study used a motion -capture system from Noraxon (myoMOTION Research Pro, Noraxon U.S.A., Inc., Scottsdale, AZ, USA, number of sensors: 2~36, myoMOTION S/W included) for acquisition of motion data from the archery athletes. The locations and directions of the inertial sensors attached to the archery athletes were as shown in Figure 1.

An inertial sensor converts changes caused by force or motion into electrical signals and provides various types of information on the object that it is attached to, such as the object's acceleration, angular velocity, speed, distance, and direction. Moreover, the advent of micro-electro mechanical systems has allowed ultra-miniaturization of these sensors. There are accelerator sensors that only detect acceleration or angular velocity, and these sensors are installed into smartphones as basic applications and have various functions in everyday life, such as using acceleration data to detect falls and monitoring breathing and sleep patterns during sleep.

Figure 1. Nine sensors are attached on the head, upper spine, left/right forearms, left/right upper arms, pelvis, and left/right shanks.

Modify Delete

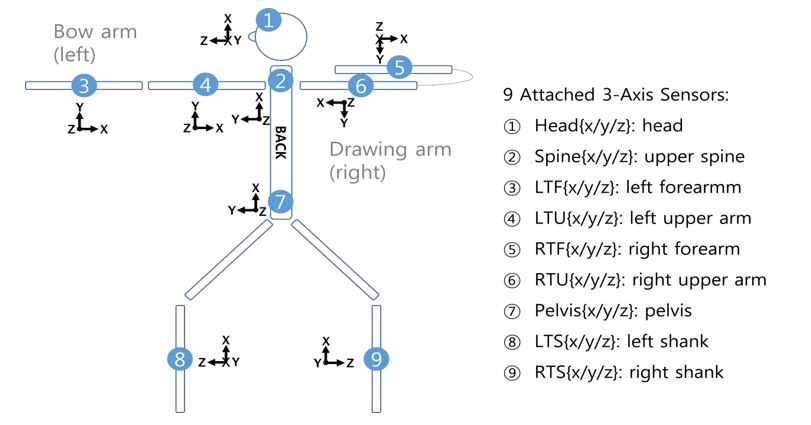
2) Data acquisition

Each participant shot six arrows consecutively while standing at the shooting line with the inertial sensors attached. The distance to the target was 30 m. After each end, meaning after all six arrows were shot (actually, about 2 min for the archery athletes to walk slowly to the target to retrieve their own arrows and prepare for the next round), a short rest was given, and then the following end began. This experiment was performed six times (ends) for each participant.

In summarizing the data acquired in the present study, since four archery athletes each shot six arrows in six ends, each athlete ended up shooting a total of 36 arrows, and thus the entire data set was 144. In each data set, motion corresponding to nine 3-axis inertial sensors (acceleration value and others) was recorded with a sampling rate of 100 Hz. However, since each of the four archery athletes shot six arrows consecutively, files were saved as ends. Therefore, the initial raw data actually used in the study comprised six files for each athlete (six ends performed) and the total for all four athletes was 24 files. From each of the files that contained six shots, data (generally six data) were extracted from the predetermined period of interest (POI) and used accordingly.

3. Data processing

1) Qualitative analysis of acceleration data during archery shooting motion

Acceleration data during archery shooting motion were qualitatively analyzed. Figure 2 shows the acceleration data of the x-axis of the bow arm (drawing direction) in the period of 21.95~42.95 sec, which was arbitrarily chosen as an example. As shown in the figure, archery shooting motion can be divided as listed below, and using the myo-MOTION S/W supplied by the motion capture system, each period was manually divided while replaying the synchronized video images. The periods were in the order of setup period (raising the bow), drawing period (drawing back the bowstring), anchoring moment (anchoring the bowstring on the face or cheek), aiming period, holding period (mentally focusing before shooting), release moment (releasing the bowstring), and follow-through period (maintaining the position even after releasing the bowstring). Moreover, although they were not in- cluded in the POI, the figure also shows motion based on bow down (lowering the bow after shooting), on the foot (immobilizing the bow’s tip on the foot), nocking (pulling the arrow from the quiver and loading), and hooking & grip (grabbing the bow and bowstring).

As shown in the figure, the POI can be set differently depending on the purpose and use, and the POI for the DTW algorithm included a part of set up, drawing, aiming, holding, and a part of follow-through periods.

The POI that defined the aiming pattern consisted of the period of about 2 sec right before the movements suddenly became larger after the arrow release. In the present study, the mean value of 200 sample acceleration data from this POI (sampling rate 100 Hz, 2 sec period) was used to define the aiming pattern. Therefore, the aiming pattern of archery athletes was defined by 27 mean acceleration values (nine 3-axis inertial sensors).

Figure 2. Example of acceleration data (21.95 s ~ 42.95 s): measured bow-forearm movement (x-axis: drawing direction) during successive archery shootings (sampling rate of 100 Hz).

Modify Delete

2) DTW-based POI extraction

DTW refers to an algorithm that searches for the optimal nonlinear mapping between two given sequences, such as acceleration data (Keogh & Ratanamahatana, 2004a). The similarity between two sequ- ences can be quantified by DTW distance (Keogh & Ratanamahatana, 2004b), and in recent times, it has been used for data fusion in multi-sensor systems (Ko, West, Venkatesh & Kumar, 2008). The DTW algo- rithm is usually used to find one or more other input data (relatively short data, referred to as reference data) from given input data (rela- tively long data, referred to as query data) in a similar period.

In the present study, the POI for defining the aiming pattern was automatically extracted, using the method below. The first attempt to analyze archery shooting motion by using the DTW algorithm was in a study by Quan, Cho, Kwon and Lee (2016). Figure 3a shows sequence Y, query data corresponding to data from one end, and sequence X, corresponding to the reference data. Figure 3b is a zoom out view of sequence X. In the process of finding sequences that are similar to the reference sequence, the DTW algorithm matches the end points between the sequences first. In Figure 3c, the end points of the searched sequences were marked with circles, and as shown, a total of six such points were found. The period representing 2 sec prior to these six end points is the POI for defining the aiming pattern.

Using the method above, 36, 35, 29, and 33 POIs were extracted from 24 files for each archery athlete and the mean acceleration was calculated to define the aiming pattern. In the first athlete only, 36 POIs corresponding to 36 arrows shot were extracted, whereas 36 POIs were not extracted in the other athletes, either because there were recording errors with the raw data or because automatic extraction by the DTW algorithm was not possible. Therefore, statistical analysis was conducted with 133 data sets, instead of 144 data sets.

Figure 3. (a) Example of input sequences for DTW: query sequence Y (109.21 s long) for one end acceleration data and reference sequence X (6.3 s long) within POI for DTW indicated by grey region. (b) Zoom out of sequence that corresponds to sequence X of (a). (c) Distance function that corresponds to top row of accumulated cost matrix. Blue small circles indicate six local minima with distance below threshold. Indices of six local minima correspond to end-point of six subsequences in Y. Grey regions indicate the POI for regression analysis.

Modify Delete

4. Stepwise multiple regression analysis

For identification of the relationship between motion in each body part immediately prior to archery shooting (independent variables) and scores (dependent variable), the SAS program (SAS 9.4, SAS Institute Inc., Cary, NC, USA) was used to performed a multiple regression analysis (29 variables: nine 3-axis sensors), and stepwise multiple regression analysis was performed to select the desired regression model. Among the many candidate regression models, the significance level of the regression models was tested and the significance level of each regres- sion coefficient was tested again to derive the final regression models with even lower significance levels, while also presenting the R2 values that indicate the explanatory power of the regression model to test the fitness of the models. And also, the regression model based on the mean data of four archery athletes was derived.

1. Regression model for subject 1

The regression model for archery athlete number 1, subject 1 (S1), was derived using the following equation:

In the derived regression model, the F value was 4.45; significance level (Pr > F) was 0.12%; R2 was 64.04%; and adjusted R2 (Adj R2) was 49.66%. Summarized parameter estimates were as shown in Table 1. The scores for S1 were explained by motions in the directions of head x-axis and z-axis, spine z-axis, left upper arm y-axis and z-axis, left forearm x-axis and y-axis, left shank y-axis, and right shank y-axis. The relative importance of scores was highest in the left upper arm y-axis motion, followed in order by left upper arm z-axis, left forearm y-axis, left forearm x-axis, left shank y-axis, spine z-axis, right forearm y-axis, head x-axis, right shank y-axis, and head z-axis.

2. Regression model for subject 2

The regression model for archery athlete number 2, subject 2 (S2), was derived using the following equation:

In the derived regression model, the F value was 4.01; significance level (Pr > F) was 1.61%; R2 was 27.934%; and adjusted R2 (Adj R2) was 20.96%. Summarized parameter estimates were as shown in Table 2. The scores for S2 were explained by motions in the directions of spine y-axis, right upper arm y-axis, and pelvis x-axis. The relative importance of scores was highest in the right upper arm y-axis motion, followed in order by spine y-axis and pelvis x-axis.

3. Regression model for subject 3

The regression model for archery athlete number 3, subject 3 (S3), was derived using the following equation:

In the derived regression model, the F value was 3.98; significance level (Pr > F) was 0.55%; R2 was 72.02%; and adjusted R2 (Adj R2) was 53.91%. Summarized parameter estimates were as shown in Table 3. The scores for S3 were explained by motions in the directions of head y-axis and z-axis, spine x-axis, left upper arm x-axis and z-axis, left forearm y-axis and z-axis, pelvis x-axis and y-axis, and left shank x-axis and z-axis. The relative importance of scores was highest in the pelvis y-axis motion, followed in order by spine x-axis, left forearm z-axis, pelvis x-axis, head y-axis, left upper arm x-axis, head z-axis, left upper arm z-axis, left shank x-axis, left shank z-axis, and left forearm y-axis.

4. Regression model for subject 4

The regression model for archery athlete number 4, subject 4 (S4), was derived using the following equation:

In the derived regression model, the F value was 4.53; significance level (Pr > F) was 0.40%; R2 was 45.62%; and adjusted R2 (Adj R2) was 35.54%. Summarized parameter estimates were as shown in Table 4. The scores for S4 were explained by motions in the directions of spine y-axis, right upper arm x-axis, right upper arm y-axis, left shank z-axis, and right shank y-axis. The relative importance of scores was highest in the right upper arm y-axis motion, followed in order by right upper arm x-axis, left shank z-axis, spine y-axis, and right shank y-axis.

5. Regression model for all subjects

The regression model based on mean data of all four archery athletes was derived using the following equation:

In the derived regression model, the F value was 56898.8; significance level (Pr > F) was 0.30%; R2 was ~1; and adjusted R2 (Adj R2) was ~1. Summarized parameter estimates were as shown in Table 5. The scores for the athletes were explained by motions in the directions of left forearm y-axis and left shank x-axis. The relative importance of scores was higher in left shank x-axis than left forearm y-axis.

1. Regression model for each athlete

In the regression equations shown in the previous section, the num- ber of independent variables included in the regression equation for each athlete was different. In other words, the number of statistically significant independent variables that influenced scores (dependent variable) was different among individual athletes (10, 3, 11, and 5). The independent variables represented data of body motions in specific directions, as measured from the points where the sensors were attached. Therefore, these results can be viewed as reflecting the characteristics of individual athletes during archery shooting motion. Consequently, habitual archery shooting motions can be reviewed by the regression parameters.

Based on a review of significance levels of regression coefficients (parameters) and regression equations derived for each athlete, the following differences in significance levels were identified. S1 showed a significant regression coefficient with a low significance level of 1.26%, while S4 showed a significant regression coefficient with a relatively high significance level of 5.10%. An interesting point was that the athletes with higher scores tended to show regression models and coefficients that were significant at relatively low significance levels. An interpretation of this finding is that, because of the nature of archery, athletes with higher scores tend to have more consistent archery shooting motion, and as a result, similar motions were observed to demonstrate that a regression equation at even a low significance level was suitable. In other words, in archery athletes who have under- gone a certain amount of training, their motions can be analyzed by deriving a regression model with the data processing and regression analysis methods used in the present study, as well as by statistical estimates, such as R2, regression coefficient, and relative importance.

With respect to R2 values, which indicate what % of variance in the dependent variable can be explained by the independent variables of the regression model, all athletes, except S2 (27.934%), showed very high values (64.04%, 72.02%, and 45.62%). Higher R2 value indicated greater number of independent variables included in the regression equation. With respect to R2 values and the number of independent variables, the athletes with R2 values of 72.02% (S3), 64.04% (S1), and 45.62% (S4) had 11 (excluding the intercept), 10, and five variables, respectively. A higher number of independent variables indicates that archery shooting motions are affected that much more by not only the lower extremities, but by the movements of the head, neck, and lower back as well. However, additional studies are needed to determine which was a more desirable archery shooting posture between S1 and S4.

Regression coefficients can indicate the degree of change in scores when the sensor attached to a corresponding area shows a motion difference of one. However, when comparing the relative importance of independent variables that comprise the regression equation to scores, the standardized estimate must be calculated. This was displayed in the last column of the summarized table of regression models derived in the previous section. Using standardized estimates enabled determin- ation of motion in specific body parts that have a greater effect on scores. Therefore, standardized estimates can serve as another key indicator for examining the habitual shooting motions of archery athletes. A comparison of relative importance (standardized estimates shown in the tables in previous section) between S1 and S4 showed that among the 11 independent variables that affected the scores of S1, the top four variables (LTUy: -1.81379, LTUz: 1.38355, LTFy: 0.88570, LTFx: -0.75727) involved motions in the bow arm (left upper and fore- arm), meaning that changes in scores can be attributed largely to motions in the bow arm. In contrast, among the five independent vari- ables that affected the scores of S4, the top two variables (RTUy: -0.60308, RTUx: 0.50498) both involved motions in the drawing arm (right upper and forearm), meaning that changes in scores can be attributed to motions in the drawing arm. In other words, the bow arm played a major role in causing changes in scores in S1, while the drawing arm did so in S4, a finding that indicates the need for different training methods for individual athletes.

An interesting point was that the highest values for relative import- ance on scores in all four athletes were all negative values, regardless of the intercept value (-1.81379, -0.42269, -1.38881, and -0.60308). This indicated that all four participants in the present study can greatly improve their scores merely by reducing the motions represented by the independent variables mentioned above.

Although the number of athletes analyzed was limited to four, based on the results above, it is believed that motions of specific body parts that affected the scores of all four athletes could be determined and that habitual archery shooting motions of each individual contributed to individual differences according to the independent variables in each regression model. The relative importance on scores could be used to determine the specific body parts that contribute greatly to each athlete's scores, and thus, development of individualized training methods for each athlete is deemed necessary.

2. Regression model using the mean values of four athletes

A regression model was derived using the mean data of four archery athletes, which showed that both the regression model and coefficients were significant at a very low significance level (0.75%) and that the motions in body parts that affected scores were LTFy (left forearm) and LTSx (left shank), meaning that the athletes' scores were largely affected by motions in the forearm of the bow arm (y-axis in up and down directions) and the left leg (x-axis in up and down directions). All four athletes used their left arm as the bow arm and used the posture of having the left foot more forward than the right foot. The relative importance results showed that leg motions had a 3.87 times greater influence than arm motions (3.86734 = 0.97252/0.25147). This indicated that all four athletes can increase their scores by maintaining improved posture by reducing movements in the legs (lower extremities), more so than the arms. The findings in the present study can be inter- preted in terms of the methods mentioned above being applicable in examination of the tendencies of a group of athletes (four in the pre- sent study), which means that they can be used to define common postural problems of athletes within the same group, or in contrast, to define a desirable posture. However, more generalized results should be derived through future studies that include larger study populations and that compare more skilled athletes.

The present study demonstrated that the relationship between aiming patterns and scores in archery shooting motions can be explained with regression models, and the following results were derived: First, the significance levels of four regression models, one for each athlete, were 0.12%, 1.61%, 0.55%, and 0.4%, which indicated that since the models showed relatively low significance levels (<2%), all of the regression models were significant; second, in the regression models, R2 values, which indicate what % of variance in the dependent variable can be explained by the independent variables of the regression model, were 64.04%, 27.93%, 72.02%, and 45.62%, and this showed that the all regression models derived, except for that of S2, had very high ex- planatory power (>40%); third, the maximum significance level of para- meters (or regression coefficients) that explain each regression model were 1.26%, 4.58%, 5.1%, and 4.98%, which indicated that parameters of all regression models derived at a significance level of 5%, with the exception of that of S3, were significant; and fourth, relative importance was presented as another key indicator for examining the habitual shooting motions of athletes.

The following conclusions were reached from a stepwise analysis of the regression models: First, different regression models were derived for each of the four athletes, which indicated that having different variables that explain the regression model means that different body parts and directions (one of three axes) affected scores, and this signi- fied that each athlete already had different habitual archery shooting motions and that individualized coaching is possible through analyses of regression model parameters and relative importance; second, the limitations in the present study were also identified. Additional future studies are needed on statistical analysis and data processing of low R2 values in the regression models and generalization of desirable archery shooting position.

Finally, statistical analysis using regression analysis and data based on the DTW algorithm, as suggested in the present study, is expected to be a useful method for the effective analysis of individualized score improvement measures in archery. Moreover, the approaches used in the present study may not only be used for motion analysis in archery, but may also have applications in various systems in the field of sports science.