The goal of speed skating is to traverse a specific distance in the shortest possible time span. To achieve this goal, speed skaters must be able to essentially distribute their energy accordingly throughout the 400 m track (Muehlbauer, Schindler & Panzer, 2010). In mid- and long-distance speed skating races, pacing strategy throughout the 400 m track plays a larger role in performance than quick start (Hettinga, De Koning, Schmidt, Wind, Maclntosh & Foster, 2011). On the other hand, explosive power, speed, quick start, and completing the race with full force are more important in the 500 m sprint race (Lee & Back, 2005; Park & Lee, 2007; Muehlbauer et al., 2010).

Studies by De Boer and Nilsen in 1989 stated that the most important technical variables in speed skating are skating posture, push-off angle, stroke frequency, and distance. The skating posture is especially impor- tant since it provides balance between minimal track frictional loss and creation of full-force expressions. In addition, the push-off angle is reportedly a crucial variable that determines the amount of work per stroke, while stroke frequency regulates speed. In curves, stroke fre- quencies are constrained by speed, stroke performance, and radius of the curve. However, stroke frequencies can be freely regulated by speed skaters on a straight track.

Among speed skating postures, push-off angle, stroke frequency, and cycle rate are identified as the most crucial performance-affecting variables to speed expression in speed skating gliding technique. From a kinematic viewpoint, posture-based performance improvement is caused by the initial stance on straight and curved tracks. In particular, acceleration from the initial stance is very important to shortening com- pletion time (Shin & Back, 1996; Back, Kwak & Chung, 2004). The initial speed skating stance is similar to the standing start stance of track and field athletes. However, speed skating incorporates a combined running-like and push-off techniques at the start signal. This motion is evident for the first 10 steps from the start line and is followed by a regular gliding and push-off technique. Therefore, speed skaters must transition to maximum speed in these first 10 steps as naturally as possible. A study by De Koning, Thomas, Berger, Groot, and Ingen Schenau in 1995 reported that when a speed skater pushes forward by fixating the push-off leg on a specific point on the track as long as possible, the push-off leg exhibits compound speed, which is composed of the toe's extension in the y-direction, and rotation, which is identical to the y-directional (horizontal) speed from the center of body mass. Once the speed skater starts relying more on the gliding technique, these two speeds start to show differences and diverge from each other. This change is observed when the average speed is 6.7 ± 0.3 m/s, which is generally reached after six step push-offs.

According to Olson (2007), skating speed is induced by the vertical force on the skate blade. Since sprint skaters start from a standing position with the skate blades on hold, push-off is performed with the skate rotated to almost 90°. Since there are no slides in the initial motions, stride length and frequency are crucial to acceleration. This motion is called impulse push, and it allows the skater to accelerate faster with faster pushes. Therefore, sprint stroke must be related to stride length and stroke frequency, and the skater must perform skate gliding at a particular point of the stroke to gain speed. In other words, skater must be able to increase the pressure of the skate while gliding for a certain amount of time and maximize pressure on the track. The increase in pressure on the track ultimately results in increased acceleration. How- ever, the impulse push in sprint skating cannot induce faster acceleration as the speed increases. Therefore, sprint skaters need to master pro- longed application of force on the track during stroke to increase speed and acceleration in a short time span.

Single leg skating, in which acceleration is induced by bearing weight on one leg at the start of sprint skating, could be the most effective technique that increases speed by producing large motions in a short time span (Olson, 2007). To transition from the initial stance to gliding, an effective combination of stride frequency and stride length are neces- sary to achieve the maximum speed in a short time span. Therefore, skating speed and distance gain, which are produced by a combination of stride frequency and stride length, are important technical infor- mation for speed skaters and should be studied since they directly affect performance.

The aim of this study is to investigate the consistency of right and left single-leg gliding and push-off posture between the start of the race and 14 steps (seven strokes). The following questions were developed for the study. First, is there a difference between the right and the left legs in terms of cycle rate and step rate of the push-off leg and the stroke trajectory? Second, at what point is the difference between the compound speed of the push-off leg and horizontal speed of the center of body observed?

1. Participants

Investigation was performed using the speed skating participants from the 49th National College Speed Skating Competition for Men and Women in 2016, hosted by the presidential committee of Korean Speed Skating Union. All participants were holding current records of 37.39 sec or less in the 500 m category, and 9.97 sec or less in the 100 m category. Total of five were selected, including three regular speed skaters and two college students. The participants had an average height of 1.80 ± 0.02 m, average weight of 76.8 ± 3.96 kg, and average record of 35.83 ± 0.30 sec.

2. Measurements

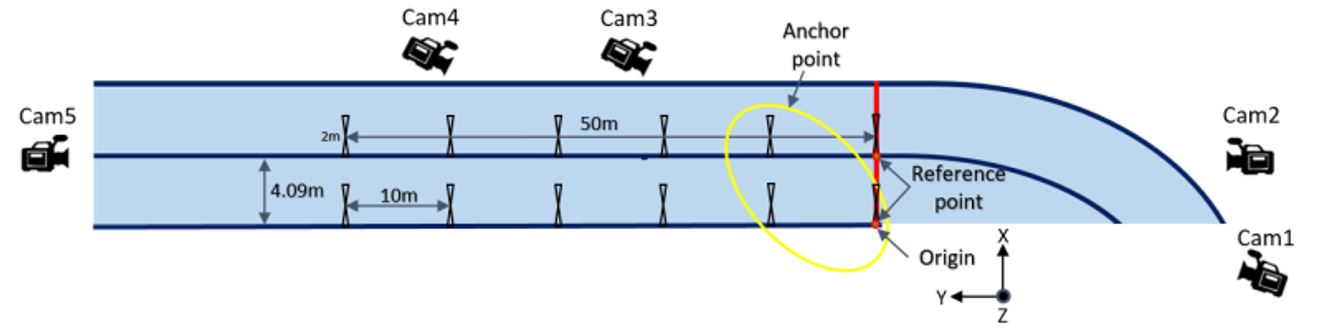
This study was conducted from the start line up to the 40-m mark of the straight portion of the track, in which a total of seven strokes were performed, and the data were analyzed. Five JVC cameras (GR-HD1KR) were installed in the audience area and the recording speed and the shutter speed were set to 60 fields/sec and 1/500 sec, respec- tively. As shown in (Figure 1), ten 2 m range poles were installed as spatial coordinates on two parallel tracks, one pole every 10 m on each 50-m long track. The poles were removed after recording and two reference marks were installed parallel to the x-axis on the start line to calculate the camera orientation angle. The reconstruction error of the digitized 28 markers was calculated as 0.02 m. Two of the five cameras were installed parallel to the skaters' direction of motion and an anchor point was set on the overlapping screens to determine the spatial coordinate of the recordings, which were overlapped to appear as a single recording. This recording method allows clearer visualization of the subject. To calculate the three-dimensional (3D) coordinates, right and left were defined as the x-axis, the direction of motion was defined as the y-axis, and vertical direction was defined as the z-axis in the world coordinate system. The cameras were synchronized by setting the 4th step of the 14 steps (seven strokes) as the synchronizing point. The Kwon 3D Version 3.1 software program was used for the synchronization.

The 3D spatial coordinates of the range pole were obtained using the direct linear transformation method as described by Abdel-Aziz and Karara (1971) and the twenty 3D coordinates in each joint were digitized using Kwon 3D Version 3.1. The participants' kinematic vari- ables were calculated using the body segment parameters reported by Plagenhoef in 1983. The digitizing errors of the 3D coordinates and the noise produced by the equipment were smoothed using the Butter- worth four-stage low-pass filter method. The cut-off frequency was set to 7.4 Hz.

Figure 1. Overview of the experimental set-up.

Modify Delete

3. Data processing

As shown in (Figure 2), the range of analysis in this study is the 40 m straight portion of the track where 14 steps (seven strokes) are per- formed. The start was defined as the moment the skater initiated move- ment. To facilitate the analysis, the events and phases after the initial stance (ready [RD]) were categorized into takeoff (TO) and touchdown (TD) including 16 events each comprising a total of 32 events. A total of 28 phases, 14 gliding and 14 cycle, were set. Phases are defined as following: step, the portion where the skater glides while one foot remains in contact with the track surface (from the TD of the foot to its TO); cycle, the portion where the skater glides after recovering from the takeoff of one foot (from the TO of the foot to its TD); stride, the portion where one foot glides followed by gliding of the other foot (from the TD of the left foot to the TO of the right foot); and stroke, cycling of both feet (from the TO of the left foot to the second TO of the right foot).

The variables analyzed in this study were location and velocity of the center of body mass, step distance, stride length, range of center of body mass and the distal feet, step frequency, stride frequency, step rate, stride rate, cycle rate, angle of the trunk and knee joints, and push-off angles between the start to the end of the seven strokes.

Figure 2. The kinematic variables of the phases (step, cycle, stride, stroke) and events (RD: ready; TO: takeoff; TD: touchdown). Plot of the toes (left: grey line; right: black lines) and trajectory of the center of mass (blue dotted line). The solid lines of the curves are the period of ice contact.

Modify Delete

This study showed that time to complete the first 100 m accounts for 28% of the total completion time of 500 m of speed skating. As the participants' performance levels increased, the time to complete the first 100 m decreased, while the average speed increased. However, high step and stride frequency do not indicate high performance level. Although the time to complete the first 100 m was not low, step and stride rates were high. The average distance traveled per step and stride showed a decreasing trend (Table 1).

(Table 2) shows that the kinematic variables during the 14 steps (seven strokes). As the duration and the average velocity of the center of mass increased, the distance after seven strokes increased. However, the step and stride rates decreased. Although participant D had high step and stride rates, the distance traveled in seven strokes was ex- cessively short.

(Figure 3) compares the horizontal and resultant velocity of the distal foot after gliding until push-off. In participant B, the two velocities sepa- rated after five steps. As for participants A, C, and E, the velocity sepa- rated after one step. For participant D, the velocity separated after two steps on the left leg but separated after six steps on the right leg (right leg only).

Figure 3. The horizontal velocity of the center of mass (solid line) compared with toe velocity of the y-direction (solid dot and dotted line) of both legs. Curves of toe velocity of the y-direction are drawn for the periods of ice contact. Note that the sign of toe velocity of the y-direction has been reversed to make a backward motion be positive.

Modify Delete

(Table 3) shows that the time required to complete the first 10 m accounts for 21% of the entire time needed to complete 100 m. The max center of mass velocity was shown to be >8 m/s when the step frequencies and cycle rates of both legs were high, such as in partici-pants A and B, or as shown in participant C, although step frequencies and cycle rates of both legs were low but the step distance was long. However, participant D, who had high bilateral step frequencies and cycle rates, had a high completion time and showed a max center of mass speed of <8 m/s. This was caused by the difference in step dis- tance where the ratio between the traveled distance and height was >83%. The cycle rates of both legs showed a higher rate on the right leg.

(Table 4) shows that the time to complete the portion between 10 m and 20 m accounts for 11% of the total time required to complete 100 m. The max center of mass velocity was shown to be >9.77 m/s when the step frequency was <3.7 and the cycle rates of both legs were <1.82 Hz as shown in participants C and E. However, similar to the first 10 m, high step frequencies and cycle rates did not indicate shorter completion time, and the max center of mass velocity was shown to be <9 m/s (participant D). This observation was also caused by the difference in the step distance where the ratio between the traveled distance and height was >151%. In this portion of the track, the cycle rate was also higher on the right leg.

(Table 5) shows that the time to complete the portion between 20 m and 30 m accounts for 10% of the total time required to complete 100 m. In this portion of the track, the completion time decreased when the step frequency decreased and the difference between the cycle rates of the two legs was small. However, the max center of mass velocity was >11.06 m/s when the step frequencies were higher than 3.3 and the cycle rates were higher than 1.73 Hz bilaterally as shown in participants A and B. This observation was also caused by the difference in the step distance where the ratio between the traveled distance and height was above 169%. Excessive step distance was shown to cause the loss of velocity. The bilateral cycle rates were almost identical as the differences decreased.

(Figure 4) compares overlapping data of the right and left knee angles during the seven strokes. With the exception of participant E, the left knee angles were observed to extend more than the right knee angles in all participants. The patterns of flexion and extension of the left and right knee angles were similar between participants A and E. Participants B and D showed a consistent pattern initially followed by an incon- sistent pattern at the latter stages. However, participant C showed an inconsistent pattern throughout the race, unlike participants B and D.

Figure 4. The overlapped right and left knee angle during the 7th stroke. Note that the sign of the marks above the curves are the instant of takeoff and touchdown.

Modify Delete

(Table 6) and (Figure 5) show that the bilateral step distance and stride distance increased with strokes, while the differences between the step distances of the left and right legs gradually decreased. The forward leaning angle of the trunk and the push-off angle also gradually decreased. However, the range of motion in the right and left directions of the center of mass was small within an average range of 0.16 m during the strokes. The range of motion of the distal feet in the right and left direction increased with decreasing lean forward angle of the trunk and decreasing push-off angle.

The lateral step distances of the 2nd stroke differed in all participants as shown in (Table 6), while the stroke trajectories were not symmetrical on the 2nd stroke. The left and right stroke trajectories on the 2nd stroke overlapped in participants C and E, where the lean forward angles of the trunk were <40°. As shown in participant D, the shapes of the stroke trajectories on the 2nd stroke showed large discrepancies when the lean forward angle of the trunk was >50° (Figure 5).

Figure 5. The position of the front end of the toe relative to the center of mass during the 2nd, 5th, and 7th strokes. The solid parts of the curves are the period of ice contact.

Modify Delete

The step distances of the right and left legs on the 5th and the 7th strokes were similar in all participants except B and D (Table 6). The stroke trajectories of the left and right legs on the 5th stroke were asymmetrical in participants D and E, while the trajectories on the 7th stroke were asymmetrical in participants B and D. Furthermore, the lean angle of the stroke trajectory varied based on the magnitude of the lean forward angle of the trunk (Figure 5).

The goal of a timed race is to improve finish time. To achieve this goal, fast acceleration and increases in speed are crucial. In track and field, velocity can be increased by increasing stride length, frequency, or rate (Mackala, 2007). However, stride length and frequency (rate) are inversely proportional to each other. The 500-m speed skating event is equivalent to the 100-m track and field race. The completion time of the first 100 m accounts for 28% of the total completion time.

The study by De Koning, Groot, & Ingen Schenau (1989) reported that the total completion time of a 500-m race is highly correlated to the completion time of the first 100 m with a correlation value of 0.88. The acceleration rate of the first 100 m reportedly affects the total completion time by 80%. Therefore, the improvement of completion time in the first 100 m is very important for improving the overall completion time.

In this study, the participants with a good completion time for the first 100 m showed high average velocity as well as higher step and stride frequencies and rates. However, their step and stride lengths were short. The results indicate that frequency and length are inversely pro- portional to each other and an optimal ratio between these two vari- ables could improve finish time.

The first 30 m is a preparation interval to reach a maximum velocity within a shortest possible time span by applying the highest acceleration. The skating motion following the start signal is running-like technique, while the push-off technique is incorporated to naturally transition to maximum velocity in 10 steps. Afterward, regular gliding and push-off techniques are used to finish the race. A study by De Koning et al. (1995) stated that the compound velocity of the skater's distal foot at push-off and the horizontal velocity of the center of mass are identical in this portion of the track. When the skater depends on gliding after this portion, the two velocities differ from each other, which is usually observed after the six steps, where the average velocity is 6.7 ± 0.3 m/s. In this study, the push-off speed of the distal foot and the hori- zontal velocity of the center of mass differed after five steps in partici- pant B versus after one step in participants A, C, and E, while only the left leg's velocities were separated after two steps in participant D and the right leg's velocities separated after six steps (only counting the right leg). Furthermore, during the first seven strokes, the traveled distance was larger with a long duration and faster center of mass velocity. However, step and stride rates were lower. These observations indicate that faster separation of the two velocities indicates dependence on gliding to accelerate.

According to Olson (2007), since there is no gliding in the initial motion, the skaters depend on stride length and frequency to accelerate. The skaters also reportedly accelerated faster with an added impulse push. Therefore, to achieve maximum velocity from the initial stance, the skaters should hone in on the impulse push technique to improve stride length and frequency.

From the start line to the 30 m mark, the completion time for the first three 10 m intervals were 21%, 11%, and 10% of the total finish time, respectively, which adds up to 42%. The study by De Koning, Groot, & Ingen Schenau (1989) reported that to improve performance, the completion time of the first 100 m is very important. Therefore, it is possible to state that improving the completion time of the first 30 m is crucial to improving the total finish time. The first 10 m from the start line shows high step frequency and bilateral cycle rates. It was also observed that, to achieve maximum horizontal velocity for center of body in the first 10 m, the step distance to height ratio must be greater than 83%. A study by Jun (2010) reported that, to quickly accel- erate the body from rest at the start line, it is important to maintain fast stroke rate and basic skating posture. A stroke that allows large space between the two legs makes it difficult for the skater to shift the center of body and accelerate. An impulse push utilizing a running-like technique at the beginning should encompass high step frequency and bilateral cycle rates utilizing high step distance to height ratio to improve finish time in the first 10 m.

In the 10 m interval between the 10 m and 20 m marks, the step frequency and bilateral cycle rates were relatively lower than the initial 10 m. However, the travel distance increased, and the maximum hori- zontal velocity of the center of body was achieved when the step dis- tance to height ratio exceeded 151%. In this interval, a combination of running-like push-off and gliding push-off techniques should be used to transition into the gliding push-off technique (De Koning et al., 1989). Therefore, to improve the acceleration of the center of body and shorten the finish time, step distance should be gained based on the step distance to height ratio and bilateral cycle rates should be increased by prompt recovery motion.

In the 10 m interval between the 20 m and 30 m marks, this is a region where regular gliding push-off technique is utilized, while the velocity could be further increased by use of the gliding technique (De Koning et al., 1995). The participants showed decreased step frequency and bilateral cycle rates in this interval. The maximum horizontal velocity of the center of body was observed when the step distance to height ratio was below 169% and the excessive step distance induced a loss of velocity. Therefore, step distance should be regulated by the step distance to height ratio.

The bilateral cycle rate was higher on the right leg up to the 20 m mark and the difference between the cycle rates between the two legs was reduced in the 10 m interval between the 20 m and 30 m marks. The difference in the cycle rates on both legs between the start and 20-m mark indicates different gliding lengths between the two legs and asymmetrical impulse push and gliding push-off. Therefore, skaters should train to equalize the cycle rates of both legs in this interval.

The forward lean angle of the trunk and push-off angles gradually decreased, while the lateral range of motion for the center of body was constant and the lateral range of motion for distal feet widened. The left knee angle was more extended than the right knee angle, while the flexion and extension patterns of the knee angles were inconsistent. Bilateral step distance on the 2nd stroke differed in all participants as shown in (Table 6), while the differences were small in the 5th and 7th strokes. The stroke trajectories were not symmetrical for the 2nd, 5th, and 7th strokes (Figure 5). The study by De Koning et al. (1995) reported that a low center of body allowed skaters a larger range of motion from the hip and knee joints that could induce a high propelling velocity on the x- and y-directions. Therefore, to quickly accelerate from the start line and transition into a regular gliding push-off motion, the center of body should be lowered, range of motion from the forward lean angle of the trunk kept small, and bilateral knee flexion and extension patterns as well as stroke trajectories kept symmetrical.

This study aimed to investigate the consistency of right and left single-leg gliding and push-off posture between the start of the race and 14 steps (seven strokes). The following questions were developed for the study. First, is there a difference between the right and left legs in terms of cycle and step rate of the push-off leg and the stroke trajec- tory? Second, at what point is the difference between the compound speed of the push-off leg and horizontal speed of the center of body observed? The following conclusion was obtained after the analysis.

The completion time of the first 100 m accounts for 28% of the total finish time, while the completion time of the first 30 m accounts for 42% of the completion time of the first 100 m. The stroke trajectories of the 2nd, 5th, and 7th strokes were asymmetrical and the flexion and extension patterns of the knee were inconsistent. The forward lean angle of the trunk cause a gradual decrease in push-off angle while stabilizing the lateral range of motion for the center of body and in- creasing the lateral range of motion for the distal feet (toe). The cycle rate of the right leg was higher between the start line and the 20 m mark in 10 m intervals, while the knee angle was more extended in the left knee angle and the bilateral gliding distances differed. The asymmetrical impulse push and gliding push-off motions differed in step rate and bilateral cycle rate of the push-off leg. Although the skating motion after the start signal depended more on the gliding push-off technique rather than a combination of running-like and push-off techniques, step and stride frequencies and rates were high, while gliding distance was short.

Skaters with a good 100 m finish record had higher step and stride frequencies and rates. However, their step and stride distances were shorter. In the interval between the start line and the 30 m mark, the compound velocity of the distal foot and the horizontal velocity of the center of body separated before an average of six step push-offs.

The results indicate that to improve the completion time of the in- terval between the start line and the 30 m mark, the trajectory of the center of body should be the base and the stroke trajectories of the bilateral distal feet should be symmetrical. While maintaining similar step rates and cycle rates on both legs, step distance to height ratio should be regulated to increase stride frequency. And finally, compound velocity of the distal push-off foot and horizontal velocity of center of body should be separated after the six step push-offs.