Open Access, Peer-reviewed
eISSN 2093-9752

Open Access, Peer-reviewed
eISSN 2093-9752
Changhyeon Eom
Jihoon You
Wang Guoyu
Sanghong Park
Jongchul Park
http://dx.doi.org/10.5103/KJAB.2025.35.2.117 Epub 2025 July 12
Abstract
Objective: The aim of this study was to develop and validate a radar-based human activity recognition algorithm using a single FMCW radar, as an alternative to conventional optical sensor-based motion analysis systems, which often present practical limitations in field settings.
Method: A total of 11 healthy adults participated in the experiment, during which 77 GHz FMCW radar and an optical motion capture system were used simultaneously. Radar signals were simulated using reflective marker position data collected from a single subject, and cross-correlation-based feature vectors were generated for training and testing. The radar signal was down-sampled in both time and range axes, and sampling parameters (e.g., sliding window length and step size) were systematically varied to evaluate classification performance.
Results: The proposed method achieved over 95% classification accuracy with the optimal radar sampling parameters (dsamp = 5, dsratio = 16) and temporal segmentation conditions (Tsamp = 0.6, dttr = 0.004). Robust performance was maintained even in noisy environments, with over 90% accuracy at SNR ≥ 5 dB. Furthermore, high generalizability was demonstrated as the system successfully recognized multiple subjects' motions using training data from a single individual.
Conclusion: The proposed FMCW radar-based motion recognition method satisfies key requirements such as accuracy, robustness, real-time processing, and data efficiency. It shows promise for practical applications in sports performance analysis, rehabilitation, and daily activity monitoring. Future studies should explore its scalability to diverse motion types and environmental conditions, as well as integration into wearable or embedded systems.
Keywords
FMCW radar Human activity recognition Cross-correlation Down-sampling Real-time processing Marker-based simulation
인간의 동작을 정밀하게 인식하고 분석하는 기술은 스포츠 과학, 재활의학, 인간-컴퓨터 상호작용 등 다양한 분야에서 중요한 역할을 하고 있다(Liu, Wang & Zhou, 2021; Vasconcelos & Tavares, 2008). 특히 스포츠 분야에서는 경기력 향상과 부상 예방을 위해 선수의 움직임을 정량적으로 측정하고 해석할 수 있는 기술의 발전이 요구되고 있다(Arzehgar et al., 2025; Penichet-Tomas, 2024). 이러한 필요에 따라, 고속 카메라와 광학 센서를 활용한 마커 기반 3차원 동작 분석 시스템이 오랜 기간 동안 표준으로 활용되어 왔다(Karatzas et al., 2024; Unger et al., 2024).
광학 센서 기반 시스템은 높은 정확도와 정밀도를 제공하지만, 복잡한 설치 과정, 높은 비용, 실내 환경 제약, 마커 부착의 불편함 등 여러 한계를 수반한다(Van der Kruk & Reijne, 2018; Yahya et al., 2019; Yuhai, Choi, Cho, Kim & Mun, 2024). 이러한 제약을 극복하기 위해 최근에는 마커를 부착하지 않는 마커리스 동작 분석 기술이 개발되고 있으며(Das, de Paula Oliveira & Newell, 2023; Song, Hullfish, Silva, Silbernagel & Baxter, 2023), 주로 영상 기반 기술이 중심이 되어왔다(Wang, 2024). 그러나 영상 기반 시스템은 촬영된 영상에서 개인의 신체 특징이 노출되기 때문에, 개인정보 보호 측면에서 근본적인 한계가 존재한다(Seifert, Grimmer & Zoubir, 2020).
이러한 문제점을 해결할 수 있는 대안으로 레이더 기반 동작 인식 기술이 주목받고 있다. 레이더는 비접촉 방식으로 동작을 측정할 수 있으며, 빛의 영향을 받지 않아 실내 · 실외 어디에서나 안정적으로 작동할 수 있다. 또한, 레이더는 대상자의 얼굴이나 신체 특징을 직접적으로 기록하지 않기 때문에 개인정보 보호 측면에서 우수한 장점을 제공한다(de Almeida et al., 2020). 이로 인해, 기존 카메라 기반 시스템에서 발생할 수 있는 윤리적 문제를 해결하고, 보다 안전한 데이터 수집이 가능하다.
뿐만 아니라, 레이더 센서는 전자기파를 빛의 속도로 방출하여 신체 움직임을 정밀하게 측정할 수 있으며(Kim, Lee, Zhang, Park & Gu, 2023), 기존 도플러 레이더에 비해 더 정밀한 주파수 변화를 감지할 수 있는 마이크로 도플러 효과를 활용하여 신체 부위별 속도 변화를 분석할 수 있다(Chen, Li, Ho & Wechsler, 2006). 이로 인해 보다 정교한 동작 인식이 가능하며, 환경적 영향을 최소화할 수 있다. 또한, 고가의 광학 센서 기반 모션 캡처 시스템과 비교했을 때 저렴하고 설치가 간편하며, 마커를 부착할 필요가 없어 보다 자연스러운 동작을 측정할 수 있다. 레이더는 넓은 탐지 범위를 갖추고 있으며(LaHaie, 2003), 주야 및 날씨 변화와 관계없이 일정한 성능을 유지할 수 있다(Sheeny et al., 2021). 이러한 장점으로 인해 레이더 기반 동작 분석 기술은 스포츠뿐만 아니라 의료 재활, 보행 분석, 보안 시스템 등 다양한 분야에서 폭넓게 활용되고 있다(Danzer, Griebel, Bach & Dietmayer, 2019).
그러나 레이더 기반 동작 인식 기술은 체형 차이, 동작 속도, 거리 변화 등에 따라 신호 반사 특성이 달라져 성능이 저하될 수 있으며, 주변 환경에 따른 다중 경로 반사나 전자기 잡음 등으로 인한 간섭에 취약하다는 한계도 존재한다(Eom et al., 2025; Kalyanaraman, Hong, Soltanaghaei & Whitehouse, 2017; Ma, Zhao Liu, Kuang & Al-Qaness, 2019). 이러한 한계는 실 환경에서의 신뢰성 확보를 위해 추가적인 보완 기술과 정밀한 신호 처리 기법이 필요함을 의미한다.
이러한 배경을 바탕으로, 본 연구는 기존의 광학 센서 기반 시스템에서 획득된 마커 좌표 데이터를 활용하여 FMCW 레이더 신호를 정밀하게 모델링하고, 이를 통해 새로운 대상자의 동작을 레이더 신호만으로도 인식할 수 있는 방법론을 제안한다. 앞선 연구에서는 5.8 GHz CW 도플러 레이더를 활용하여 10명의 대상자에게서 마커 위치 데이터를 기반으로 생성한 레이더 신호와 실제 대상자의 정면에서 직접 측정한 레이더 신호 간의 상호 상관을 통해 특성 벡터를 추출하였다. 추출된 특성 벡터는 학습 데이터와 시험 데이터로 나누어 동일 대상자에 대해 동작 인식 성능을 평가하는 데 사용하였다. 이를 통해 레이더 기반 동작 인식의 가능성을 확인할 수 있었으나, 실제 활용을 위해서는 대상자에 대한 일반화 성능 확보가 필요하다는 한계가 있었다(Eom et al., 2025). 본 연구에서 활용된 FMCW 레이더는 앞선 연구에서 사용한 CW 레이더와 달리, 송신 주파수를 시간에 따라 변조함으로써 측정 대상의 거리 정보를 동시에 획득할 수 있는 보다 정밀한 레이더이다(Piotrowsky, Jaeschke, Kueppers, Siska & Pohl, 2019).
이에 따라 본 연구에서는 한 명의 대상자에게서 획득한 학습 데이터를 기반으로 새로운 대상자의 레이더 반사 신호를 분석하고 인식할 수 있는 알고리즘을 설계하여 기존 기술의 실용성을 한층 높이고자 한다. 또한 대규모 딥러닝 모델 대신 비교적 간단한 cross-correlation 기반의 특성 벡터 추출 방식을 활용하고, 시간-주파수 영역에서의 신호 특징을 효과적으로 벡터화함으로써 높은 인식률을 달성할 수 있는 방법론을 제시한다.
1. 연구 대상
본 연구는 6개월 이내 상하지 근골격계에 부상이 없는 남자 6명과 여자 5명, 총 11명의 건장한 성인을 대상으로 시행하였다. 본 실험은 본교 생명윤리위원회로부터 승인을 받았으며(IRB 승인번호: 2025-03-004), 본 실험에 참여한 모든 피험자들은 실험에 참여하기 전 실험 과정에 대한 설명과 참여의사 동의서를 받았다. 연구 대상자의 특성은 <Table 1>과 같다.
|
Variables (m ± sd) |
Male (n = 6) |
Female (n = 5) |
|
Age (years) |
27.00±3.16 |
24.20±3.49 |
|
Height (cm) |
173.65±5.72 |
163.50±4.72 |
|
Weight (kg) |
82.17±8.73 |
53.00±6.52 |
2. 실험장비 및 절차
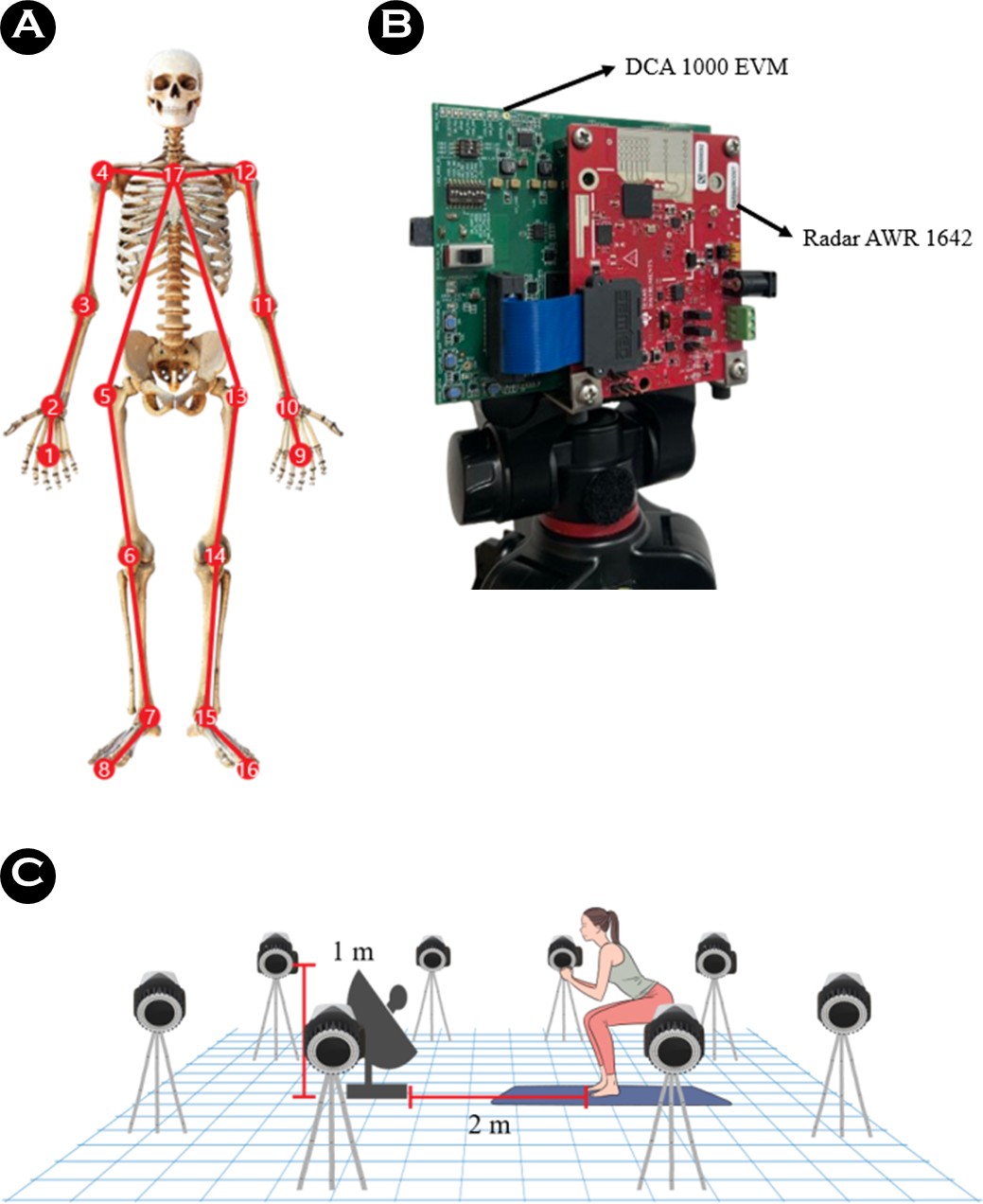
본 연구에서는 8대의 적외선 카메라(Miqus M5; Qualisys AB, Gothenburg, Sweden, sampling rate 250 Hz)를 활용하여 인체에 부착된 반사 마커의 위치 데이터를 수집하였다. 데이터 수집에는 QTM (Qualisys Track Manager; Qualisys, Gothenburg, Sweden) 프로그램을 사용하였으며, 실험 공간의 3차원 좌표계(X축: 좌우, Y축: 전후, Z축: 수직)는 NLT (non-linear trans- formation) 방식의 캘리브레이션(calibration)을 통해 설정하였다. 실험 참가자는 스판덱스 소재의 타이즈 상하의를 착용한 상태에서, 레이더 측정 시 전자파가 반사되는 산란점을 고려하여 <Figure 1.a>와 같이 인체에 총 17개의 반사 마커를 부착하였고, 레이더와 마커 사이의 거리를 계산하기 위해 레이더 중앙에 1개의 마커를 부착하였다. 레이더 측정에는 77 GHz FMCW (frequency modulated continuous wave) 레이더인 AWR 1642 (Texas Instruments, Dallas, USA)를 사용하였으며, 데이터는 DCA 1000 EVM (Texas Instruments, Dallas, USA) 모듈을 통해 노트북으로 수집하였고(<Figure 1.b> 참조), mmWave Studio (Texas Instruments, Dallas, USA) 프로그램을 통해 bin 파일로 획득하였다. 레이더는 피험자로부터 전방 2 m 거리에서 정면을 향해 배치되었으며, 측정 높이는 <Figure 1.c>와 같이 1 m로 설정하였다. 레이더의 세부 파라미터는 <Table 2>에 제시하였다. 실험 전, 피험자들은 부상 방지를 위해 10분간 준비운동을 진행하였으며, 이후 <Figure 2>와 같은 5가지 기본적인 상 · 하지 운동 동작을 수행하였다. 동작은 스마트폰 어플을 활용하여 60 BPM (beat per minute)으로 설정된 메트로놈 소리를 스피커로 출력하며 진행되었다. 피험자는 4초 동안 한 번의 동작을 완료하도록 유도되었으며, 스쿼트를 제외한 나머지 네 가지 동작은 좌우를 번갈아 수행하였다. 측정은 적외선 카메라를 활성화시킨 후 BPM에 맞추어 동작을 수행하였고 왼측부터 시작된 마지막 동작 2회에 8초간 레이더를 활성화하여 측정한 후 동작을 종료하였다.

|
Parameter |
Numerical
parameter numerical |
|
Initial frequency |
77 GHz |
|
Transmitting antenna |
1 pc |
|
Receiving antenna |
1 pc |
|
FM slope rate |
29.982 MHz/µs |
|
Sampling frequency |
6 MHz |
|
Total number of frames |
200 frames |
|
FM bandwidth |
3.897 GHz |
|
Chirp/frame |
250 |
|
Duration |
8 sec |
|
Sampling points/chirp |
512 |
3. 자료 처리
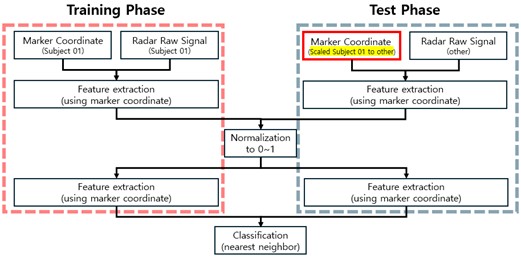
본 연구에서는 이전 연구와 동일한 방식으로 마커 기반 모션 캡처 데이터를 활용하여 레이더 신호를 시뮬레이션하고(Eom et al., 2025), 이를 통해 <Figure 3>와 같이 학습 및 시험 데이터를 구성하였다. 자료 처리는 레이더 신호 생성, 학습 데이터 구성, 시험 데이터 구성의 세 단계로 이루어졌으며, MATLAB R2023b (MathWorks, Natick, Massachusetts, USA) 환경에서 구현되었다.
1) 레이더 신호 생성
수집된 bin 파일은 FMCW 레이더의 물리적 신호 모델을 기반으로 처리되었다. 시간에 따라 주파수가 선형적으로 증가하는 chirp 신호는 반사되어 다음과 같은 Beat 신호로 수신된다.
여기서 j=√(-1), f_b=2kr(t)/c,λ=c/f_c ,r(t)는 시간에 따른 대상자 거리이다. c=3×10^8으로 빛의 속도를 의미한다(Table 3 참조).
| Parameter | Value |
|---|---|
| j | √−1 |
| fc | 77.0000 GHz |
| c | 3 × 108 m/s |
| λ | 0.0039 m |
레이더 데이터는 총 n=50,000개의 chirp과 n=512개의 fast-time 샘플로 구성되어 있으며, 복소수 행렬 S∈C^(n×m) 형태로 로딩된다.
(1) 시간 축 Down-sampling
데이터 처리량을 줄이고 실시간성에 근접한 분석을 위한 시간 축 slow-time 방향에서 일정 간격 d_samp으로 down-sampling을 수행하였다.
(2) 거리 변환 및 관심 구간 지정
Down-sampling된 신호 S_ds의 각 chirp에 대해 fast-time 방향으로 1차원 FFT를 적용하고, fftshift를 통해 중심 주파수 기준으로 거리 정보를 재배열하여 거리-시간 행렬 RP를 구성하였다.
이때 거리 bin은 음의 거리부터 양의 거리까지 대칭적으로 재배열된다. 총 m=512개의 거리 bin은 거리 해상도 ∆R=c/2B≈0.0385 m 기준으로 약 ±9.85 m 범위를 커버하며, 중앙 bin은 k_0=⌊m/2⌋=256에 해당한다(Figure 4 참조).
① 거리 축 down-sampling
연산의 효율을 높이기 위해, 전체 거리 bin 중 중심 기준으로 일정 비율만 남기는 거리 방향 down-sampling을 수행하였다.
이 과정을 통해 축소된 신호 S_cut에 대해 다시 FFT 및 fftshift를 적용하여 down-sampled 거리 프로파일 RP_ds를 구성하였다.
② 초과 거리 제거 및 최대 에너지 bin 선택
그 다음, 실험 설정에 따라 의미 없는 거리(2.5 m 초과)에 해당하는 bin은 제거하였다.
이때 거리 해상도와 down-sampling 비율을 고려하여 2.5 m 이내에 해당하는 bin 수는 음의 구간까지 합하여 다음과 같이 계산된다.
따라서 최종적으로 분석에 사용된 거리 프로파일은 다음과 같이 정의된다.
이후 RP_final에서 시간 축 전체를 기준으로 가장 높은 에너지를 가진 거리 bin k^*를 선택하여, 해당 거리 bin의 시간 신호를 최종 레이더 신호로 사용하였다.
2) 학습 데이터 구성
(1) 마커 기반 시뮬레이션 신호 생성
11명의 대상자 중 남성 대상자 1명(age: 26 years, height: 181 cm, weight: 96 kg)의 마커 위치 데이터를 기준으로, 각 마커(=k)와 레이더 간 거리 r_k (t)를 계산하고, 이를 기반으로 Beat 신호를 시뮬레이션 하였다(Table 3 참조).
총 17개의 마커에 대해 생성된 신호는 MS∈C^(17×n) 형태로 구성되며, 마커 기반 시뮬레이션 신호는 실제 레이더 신호의 시간 해상도와 일치시키기 위해 선형 보간을 수행하였다. 보간은 마커 데이터의 원본 샘플링 간격과 레이더 chirp 간격의 불일치를 보완하기 위해 동일한 시간 축으로 재배열하는 방식으로 진행되었다. 또한 상체 동작 수행 시 하지에 부착된 마커의 움직임과 하지 동작 수행 시 상지에 부착된 마커의 움직임이 거의 없거나 정지 상태인 구간에서 발생할 수 있는 신호 왜곡을 최소화하기 위해 전체 시뮬레이션 신호에 대해 1차 미분 처리를 적용하였다.
(2) 특성 벡터 생성
레이더 신호 RS와 마커 기반 신호 MS_k는 길이 <Figure 5>와 같이 T_len=n×T_samp의 구간으로 슬라이딩 분할되었고, 이동 간격은 T_step=n×dt_tr로 설정되었다.
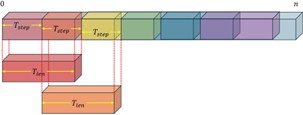
여기서 t_i=(i-1)∙T_step이고, i는 슬라이딩 윈도우 구간 번호를 뜻한다. 해당 과정을 통해 전체 시간에서 총 n_tr= (n-T_len)/T_step개의 윈도우가 형성된다.
그 후 각 구간의 신호를 L2-norm 정규화 후 cross-correlation을 통해 유사도를 계산하였으며, 마커별 최대 상관값을 특성으로 정의하였다.
본 연구에서는 cross-correlation coefficient의 시계열 중에서 각 마커별 최대값을 대표값으로 사용하고, 이를 순차적으로 배열하여 17차원 특성 벡터 f^((i))∈R^(1×17)를 구성하였다. 이렇게 생성된 특성 벡터는 학습 데이터 F_train으로 사용되어 각 동작 별 학습 데이터 셋을 형성하였다.
3) 시험데이터 구성
(1) 스케일 보정 기반 마커 신호 생성
시험 데이터는 1번 피험자를 제외한 10명의 피험자 데이터를 기반으로 하였으며, 각 피험자의 첫 번째 프레임만을 사용하였다.
레이더 신호 시뮬레이션에 있어 마커의 절대 위치 정보가 핵심이므로, 피험자 간의 신체 크기 차이로 인해 발생할 수 있는 왜곡을 보정하기 위한 절차가 필요하다. 이를 위해 기준 대상자(1번)의 마커 간 상대 벡터를 참조로 하여, 개별 피험자의 마커 위치를 스케일 보정하였다.
먼저, 기준 대상자의 두 마커 M_k^ref,M_l^ref∈R^3 간의 거리와 시험 대상자의 동일한 마커 쌍 M_k^test,M_l^test∈R^3 간의 거리 비율을 이용하여 보정 계수 φ_kl를 계산하였다.
계산된 φ_kl를 활용하여, 시험 대상자의 마커 위치 M_k^test를 기준 마커 M_l^test로 부터 상대 벡터 방향은 유지하되, 크기만 기준 대상자에 맞추어 재조정하였다. 최종 보정된 마커 위치는 다음과 같이 정의된다.
이러한 방식으로, 각 시험 대상자에 대해 모든 마커 위치가 기준 대상자의 체형에 맞추어 스케일 보정되며, 이를 기반으로 레이더와의 거리 정보를 계산하여 시뮬레이션 신호 MS_k (t)를 생성하였다. 신호 생성은 학습 데이터 구성과 동일한 식 (6)으로 이루어졌다.
(2) 특성 벡터 추출 및 구성
시험 데이터 역시 슬라이딩 윈도우 방식으로 분할된 후, cross-correlation을 통해 마커 기반 특성 벡터를 생성하였다. 이후 총 5개 동작 각각에 대해 50개의 특성 벡터를 무작위로 추출하여 시험 데이터 셋을 구성하였다.
4) 학습 데이터와 시험 데이터 정규화
본 연구에서는 정규화의 일관성을 유지하고 모델의 일반화 성능을 높이기 위해, 학습 데이터와 시험 데이터를 별도로 정규화하지 않고, 전체 데이터 셋에서 계산된 공통의 최소값 f_min과 최대값 f_max을 사용하여 모든 특성 벡터를 정규화하였다. 정규화는 다음 min-max 방식으로 적용되며, 각 마커 k에 대해 공통 수식을 따른다.
이 방식은 학습/시험 데이터 간 스케일 차이를 제거하고, 특성 벡터 간 상대적인 비교 및 분류 정확도를 안정적으로 확보하는 데에 기여하였다.
5) 동작 분류 방식
두 시험 데이터와 학습 데이터의 특성 벡터들은 유클리디안 거리를 기반으로 분류되었다. 각 시험 벡터는 모든 학습 벡터와의 거리를 계산하며, 가장 가까운 벡터가 속한 동작 클래스 a로 분류된다. 여기서 a는 클래스 index를, b는 해당 클래스 내 개별 학습 샘플 index를 의미한다. 유클리디안 거리는 다음과 같이 정의된다.
최종 분류 결과는 다음과 같이 결정된다.
전체 250개의 시험 벡터에 대해 분류를 수행하고, 참값과 비교하여 혼동 행렬을 구성하였다. 분류 정확도는 다음과 같이 계산된다.
여기서 C는 혼동행렬(confusion matrix)이며, 대각 원소(trace(C))는 정확히 분류된 샘플 수를 의미한다.
4. 레이더 샘플링 파라미터와 시험 데이터 및 학습 데이터 특성
본 연구에서는 레이더 신호 처리 단계에서의 down-sampling 파라미터 및 특성 벡터 생성 시의 시간 분할 조건에 따른 동작 분류 성능의 변화를 분석하고자 하였다. 이를 위해 레이더 신호의 시간 축 및 거리 축 down-sampling 비율과, 특성 벡터 생성을 위한 슬라이딩 윈도우 길이 및 간격을 다양한 조건으로 조절하며 실험을 수행하였다.
1) 레이더 샘플링 파라미터 설정
레이더 신호 처리 단계에서 식 (2)의 시간 축 down-sampling 간격 d_samp와 식 (4)의 거리 축 down-sampling 비율 ds_ratio를 조절하였다. 다음의 5가지 조건 조합을 설정하여 총 5 × 5 실험을 진행하였다.
시간 축 down-sampling 간격 d_samp={5,10,15,20,25}
거리 축 down-sampling 비율 ds_ratio={2,4,8,16,32}
각 조합마다 동일한 방식으로 레이더 신호를 처리하고, 거리 bin 중 최대 에너지를 갖는 지점을 기준으로 시간 신호 RS를 추출하였다. 이후 동일한 방식으로 학습 및 시험 특성 벡터를 구성하여 분류를 수행하였으며, 정확도 변화를 비교 분석하였다. 이때의 특성 벡터 구성은 T_samp=0.2,dt_tr=0.002로 설정하여 n_tr=400이다.
2) 학습 및 시험 데이터 시간 분할 조건
학습 및 시험 데이터의 특성 벡터 구성 과정에서는 3.2)(2) 절에서의 슬라이딩 윈도우의 길이 T_samp와 슬라이딩 간격 dt_tr을 조절하여, 신호 분할 방법에 따른 분류 성능 변화를 분석하였다. 이때의 d_samp와 ds_ratio는 이전 결과에서 가장 높은 정확도를 보인 값으로 설정하였다. T_samp와 dt_tr의 변수는 다음과 같으며 해당 변수에서의 n_tr은 <Table 4>와 같다.
| dttr | |||||
|---|---|---|---|---|---|
| Tsamp | 0.002 | 0.004 | 0.006 | 0.008 | 0.010 |
| 0.2 | 400 | 200 | 133 | 100 | 80 |
| 0.3 | 350 | 175 | 116 | 87 | 70 |
| 0.4 | 300 | 150 | 100 | 75 | 60 |
| 0.5 | 250 | 125 | 83 | 62 | 50 |
| 0.6 | 200 | 100 | 66 | 50 | 40 |
윈도우 길이 T_samp={0.2,0.3,0.4,0.5,0.6}
슬라이딩 간격 dt_tr={0.002,0.004,0.006,0.008,0.01}
5. 잡음의 영향 분석
본 연구에서는 최종적으로 도출된 최적 조건의 성능을 평가하기 위해, 가산 백색 잡음(additive white Gaussian noise, AWGN)을 신호 대 잡음비(signal-to-noise ratio, SNR) 0 dB부터 20 dB까지 5 dB 간격으로 부가하여 구분율 변화를 분석하였다(Tian, Bai & Zhou, 2023). 다만, 이러한 무작위 잡음 부가 방식은 실제 환경에서 발생할 수 있는 다양한 잡음 및 간섭을 완전히 반영하지 못한다는 한계가 있다. 따라서 향후 연구에서는 실제 환경 조건에서의 동작 인식 정확도를 검증하는 추가 실험이 필요할 것으로 판단된다.
총 5 × 5 조건에 대해 학습 및 시험 특성 벡터를 각각 구성하였으며, 각 조건에서 분류 정확도와 학습 및 시험 데이터 형성에 소요되는 시간을 산출하여 비교하였다. 본 설정은 시간 분해능과 학습 데이터의 다양성 확보 정도가 분류 성능에 미치는 영향을 평가하기 위한 목적으로 설계되었다.
1. 레이더 파라미터 설정에 따른 정확도
레이더 측정 신호의 시간 축과 거리 축에 대한 다운 샘플링의 영향 분석 결과는 <Figure 6>에 제시하였다. 이때 정확도는 동일한 조건에서 한 명에게서 획득한 학습 데이터를 기반으로, 10명의 대상자에 대해 산출한 혼동 행렬을 식 (17)을 이용하여 계산한 뒤, 그 10개 정확도의 평균값으로 표현하였다. 거리 축의 down-sampling 비율을 결정하는 변수인 ds_ratio는 식 (4)의 거리 bin 수 M=512를 기준으로 bin 수를 감소시키며, ds_ratio가 증가할수록 유지되는 bin 수, ds_end는 작아진다. 실험 결과, ds_ratio가 클수록 즉, 거리 해상도는 낮아지지만 더 높은 분류 정확도를 보이는 경향을 확인할 수 있다.
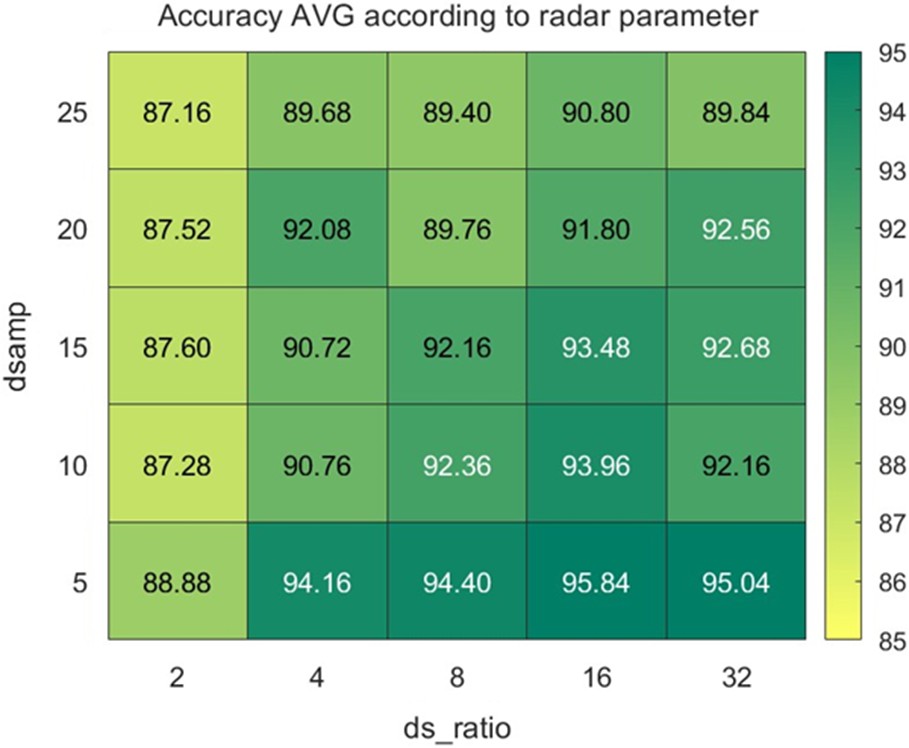
반면, 시간 축의 down-sampling을 의미하는 d_samp는 식 (2)의 총 chirp 수 n=50,000에서 유효 chirp 수를 줄이는 역할을 하며, d_samp가 커질수록 n은 작아진다. 해당 결과에서는 d_samp가 작아질수록 즉, 더 많은 시간 해상도를 유지할수록 분류 정확도가 향상되는 경향을 나타내었다. 이중 d_samp=5,ds_ratio=16에서 95.84%의 가장 높은 정확도가 나타났다.
2. 학습 및 시험 데이터 시간 분할 조건에 따른 정확도
이전 레이더 파라미터 설정에서 가장 높은 정확도를 보인 dsamp=5,ds_ratio=16 조건에서 학습 및 시험 데이터 생성 시 시간 분할 조건인 T_samp와 dt_tr의 변화에 따른 결과를 <Figure 6>과 동일한 방식으로 계산하여 <Figure 7>에 제시하였다. T_samp는 샘플링 하는 시간 길이를 뜻하며 T_samp가 클수록 시간 구간이 길어진다. 이때의 결과는 T_samp=0.6에서 정확도 95% 이상이 나타난 것을 확인할 수 있다.
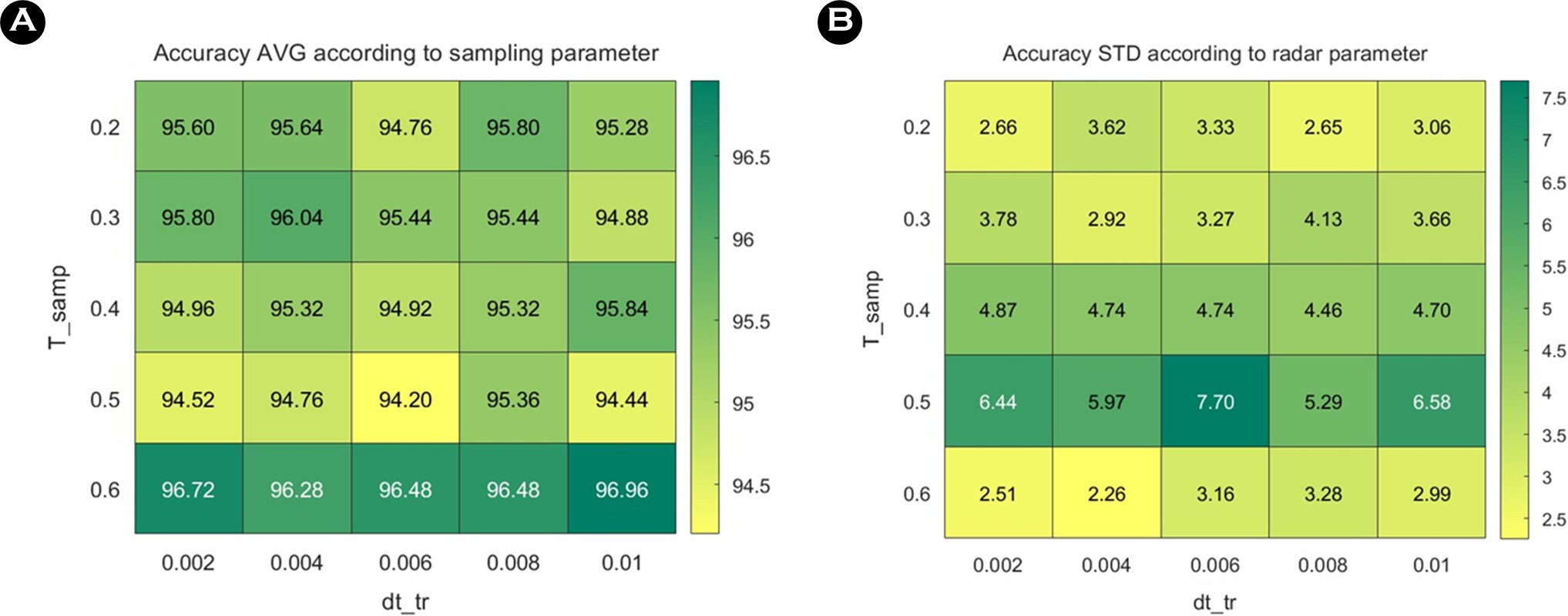
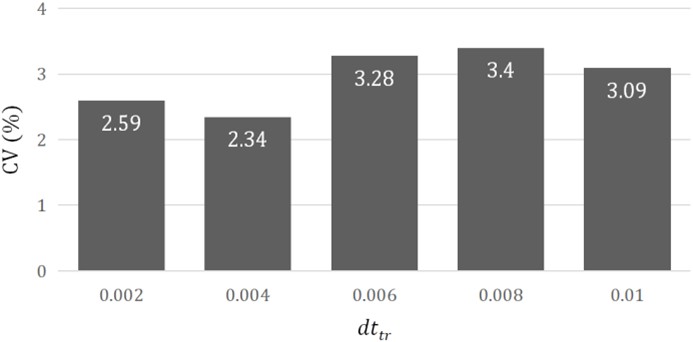
dt_tr은 샘플링 시 슬라이딩 간격을 뜻하며 이는 커질수록 슬라이딩되는 길이가 길어지며 n_tr의 개수가 작아진다. 이때의 결과는 큰 차이를 나타내지 않았으며 95% 이상의 정확도를 보인 T_samp=0.6에서 dt_tr에 따른 CV=(STD/AVG)×100를 확인하였으며 결과는 <Figure 8>과 같다.
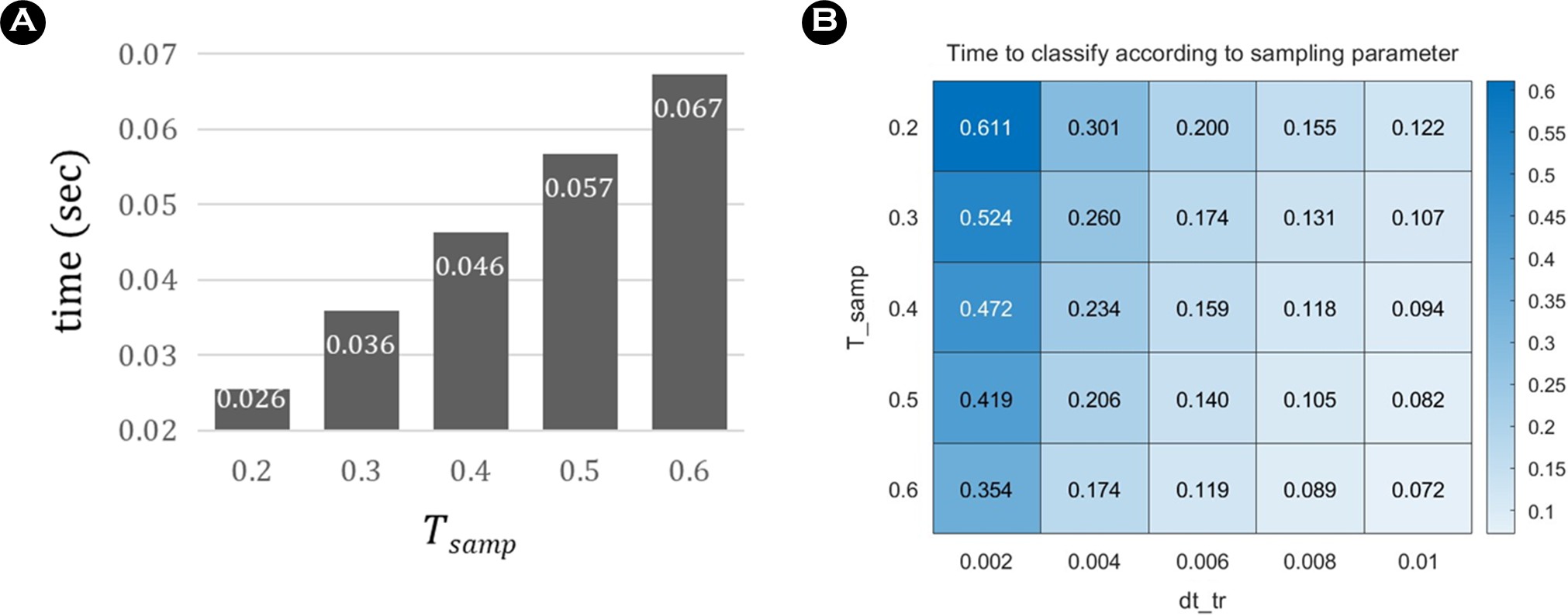
1) 시간 분할 조건에 따른 시험데이터 형성 시 소요되는 시간과 식별 시 소요되는 시간
시험 데이터 생성 시 T_samp에 따라 하나의 데이터가 형성되는 시간은 각 조건에서의 전체 형성 시간의 평균값을 바탕으로 <Figure 9.a>에 나타나 있다. 각 동작당 50개의 데이터, 총 250개의 시험 데이터를 추출하므로, 데이터 형성 시간은 dt_tr의 영향을 받지 않으며 T_samp에 의해서만 결정된다. 이에 따라 T_samp가 커질수록, 즉 샘플링 주기가 길어질수록 데이터 형성에 소요되는 시간도 증가하는 경향을 보였다.
학습 데이터와 시험 데이터 간 비교를 통해 식별에 소요되는 시간은 <Figure 9.a>와 같은 방식으로 <Figure 9.b>에 제시되어 있다. 이 결과로부터 T_samp와 dt_tr 값이 작아질수록 식별에 필요한 시간이 더 길어지는 경향이 있음을 확인할 수 있었다.
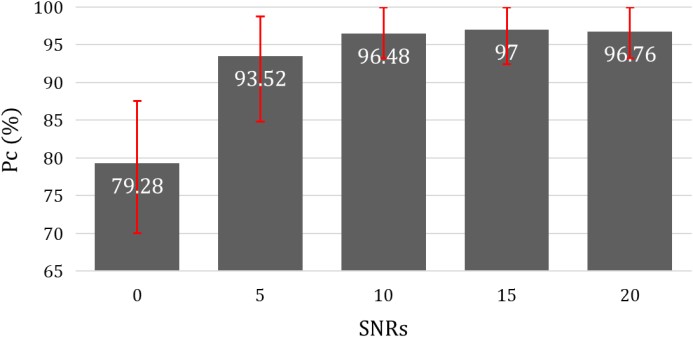
3. SNR (signal to noise ratio)에 따른 정확도
이전 실험 결과를 바탕으로, 95% 이상의 정확도를 보인 T_samp=0.6과 CV가 2.34%로 안정적인 성능을 나타낸 dt_tr=0.004 조건에서 SNR에 따른 성능 변화를 비교하였다. 이에 대한 결과는 각 조건에서의 전체 평균을 바탕으로 <Figure 10>에 제시되어 있다. SNR이 낮을수록, 즉 잡음이 많이 첨가될수록 분류 정확도가 감소하는 경향을 보였다. 그러나 SNR이 10 이상인 경우, 잡음이 없는 환경과 유사하게 95% 이상의 정확도를 유지하는 것으로 나타났다.
본 연구는 기존 광학 센서 기반 동작 분석 시스템의 한계를 극복하고자 FMCW 단일 레이더를 활용한 다중 대상자의 동작 인식을 시도하였다. 하나의 레이더의 출력 값은 해당 동작에서 반사된 모든 산란점 신호의 합으로 나타나게 되어 운동학적 변인을 산출할 수 있는 동작 분석 시스템에는 한계가 있다(Liu, Zhang & Liu, 2024). 그러나 단일 레이더로 추출한 스포츠 동작의 신호 특징들을 비교하는 것이 가능하다면 추후 연구를 통해 레이더를 활용한 스포츠 현장에서의 동작 분석 시스템이 가능할 것으로 판단된다. 이전 Hadjipanayi 등 (2024)의 연구에 따르면 다중 레이더의 미세도플러를 활용하여 보행 시간, 디딤기와 흔듦기 시간, 분당 걸음 수와 같은 시간적 매개변수를 획득하였으며, 이는 다중 레이더를 활용한 동작 분석의 잠재력을 나타내는 것이라 할 수 있다.
본 연구는 하나의 학습 데이터를 활용하여 다중 대상자의 레이더 신호만을 활용한 동작 인식 시스템을 개발하고자 시행되었고, 이전에 선행되었던 Eom 등 (2025)의 연구에 따르면 5.8 GHz CW 도플러 레이더를 활용한 동작 인식 정확도를 검증하였다. 그러나 이때 학습 데이터와 시험 데이터에 활용되었던 특성 벡터가 동일한 대상자의 마커 위치 데이터와 레이더 신호 데이터를 활용하여 생성되었기 때문에 실제 환경에서의 동작 인식 시스템을 시행하는데 부적합하다고 판단되었다. 이에 본 연구에서는 한 명의 대상자에게서 획득한 마커 위치 데이터를 기반으로 다른 대상자의 신체 크기에 따라 마커 위치 데이터의 크기를 조절하여 특성 벡터를 형성하였으며 이를 통해 측정하는 대상자는 신체 사이즈와 레이더 신호만 있으면 동작 인식이 가능하게 된다.
본 연구의 동작 인식 기법은 이전 Eom 등 (2025) 연구와 동일하게 두 신호의 상호 상관을 통한 최댓값으로 형성된 특성 벡터를 통해 진행되었으며 이때의 각 신호는 데이터 형성 및 식별 시간을 최소화하기 위해 원 신호를 활용하여 진행되었다. 본 연구는 이전 연구와 다르게 더 높은 해상도의 77 GHz의 FMCW 레이더를 활용하였으며 <Table 2>의 레이더 파라미터 설정 값에 따라 50,000개의 시간 해상도와 512개의 거리 해상도로 측정되었다. 이때 시간 해상도 50,000개의 신호를 모두 활용하게 되면 많은 데이터 양으로 인해 데이터 처리에 소요되는 시간이 오래 걸리게 되며 이를 위해 d_samp에 따라 다운 샘플링을 진행하였다(Van Der Donckt, Van Der Donckt & Van Hoecke, 2025). <Figure 6>과 같이 d_samp=5일 때, 가장 높은 정확도를 보였으며 d_samp가 커질수록 정확도는 떨어지는 것을 확인할 수 있었다. 이는 d_samp가 작을수록 더 높은 시간 해상도가 유지되어 미세한 신체 동작에 의해 발생하는 신호의 주기성 및 패턴 변화가 손실 없이 보존되며, 이는 상호 상관 기반 특성 벡터가 보다 뚜렷한 피크 값을 가지도록 만들어 정확도 향상으로 이어졌음을 나타낸다(Long et al., 2019). 반면, 과도한 다운 샘플링은 신호를 손실 없이 재구성하기 위해 필요한 최소 샘플링 주파수인 나이퀴스트 주파수를 초과하게 해 신호가 왜곡되는 에일리어싱 현상을 유발하여 신호가 손실되고, 이는 동작 간 패턴 분별력을 저하시켜 정확도 감소의 원인이 되었음을 시사한다(Stump, 2014).
512개의 거리 해상도에서는 이전 Eom 등 (2025)의 연구와 동일한 미세도플러 신호를 추출하기 위해 전체 해상도 중 하나의 bin을 추출하여야 한다. 이때 하나의 bin은 레이더 파라미터에 따라 약 0.0385 m의 거리를 커버하므로, 대상자의 전체 움직임 범위를 포착하지 못하게 된다. 이러한 현상은 거리 모호성(range ambiguity)이라고 하며, Horiuchi, Hoshino, Oishi와 Suwa (2021)은 압축 센싱 기반의 SAR 영상 복원 및 도플러 스펙트럼 분석을 통해 PRF 다운 샘플링에서 발생하는 방향 모호성을 효과적으로 구별한 바 있다. 본 연구에서는 이와 유사한 방식으로 거리 축에 다운 샘플링을 적용하여 거리 모호성을 완화하고자 하였다. 다운 샘플링은 ds_ratio에 따라 진행되었으며, <Figure 6>에서 나타낸 바와 같이 d_samp=5 조건에서 ds_ratio가 16 이상일 때 95% 이상의 정확도를 보였다. 이는 ds_ratio가 증가함에 따라 하나의 bin이 커버하는 거리 범위가 넓어지고, 이로 인해 보다 높은 정확도를 달성했음을 시사한다.
학습 데이터 및 시험 데이터의 특성 벡터 형성을 위한 샘플링 길이 조절에 따른 결과는 <Figure 7>과 같다. 전체적인 정확도는 90%를 초과하였으며 dt_tr의 변화가 정확도에 큰 영향을 나타내지 않음을 나타냈지만 T_samp=0.6에서 96% 이상의 정확도를 보이며 전체 범위에서 높은 정확도를 나타내었다. 이전 Zuo, Tang과 Zhou (2020)의 연구에 따르면 샘플링 길이가 짧을 경우 프랙탈 차원의 추정 정확도가 낮아지며, 충분한 샘플링 길이를 확보해야 안정적인 추정이 가능하다고 보고하였다. 이는 슬라이딩 윈도우 방식의 샘플링에서도 윈도우 크기를 적절히 설정하는 것이 중요함을 시사한다.
본 연구는 하나의 학습 데이터를 활용하여 여러 대상자의 동작 인식 정확도를 검증하고, 대상자의 동작을 통해 실시간 동작 인식의 가능성을 판단하고자 하였다. 이를 위해 하나의 시험 데이터를 형성하는 데 소요되는 시간과, 하나의 동작이 식별되는 데 소요되는 시간을 수집하였다. 이때 dt_tr은 동작당 학습 데이터 개수에 영향을 미치는 변수이므로, 시험 데이터 형성 시간에서는 T_samp의 영향만을 분석하였다.
<Figure 9.a>에 나타난 바와 같이, T_samp=0.2일 때 평균 0.026초로 가장 빠르게 시험 데이터가 형성되었으며, T_samp가 커질수록 하나의 샘플이 포함하는 시간 길이가 증가하여 더 많은 시간이 소요되는 것을 확인할 수 있었다. 이는 샘플 길이가 짧으면 더 빠른 데이터 분할과 처리 단계가 가능하다는 것을 의미하며, 이는 Zuo 등 (2020)이 보고한 바와 같이 샘플 길이가 늘어나면 처리 연산량이 증가하여 계산 시간이 길어진다는 기존 연구와 일치한다.
한편, 하나의 동작이 식별되는 데 소요되는 시간은 <Figure 9.b>에 제시되어 있으며, 이는 <Table 4>의 n_tr 값에 따라 달라지는 양상을 보였다. n_tr이 증가함에 따라 비교에 사용되는 학습 데이터의 수가 많아지기 때문에 상호 상관 연산 횟수가 증가하고, 이에 따라 처리 시간이 선형적으로 증가하였다.
반대로 n_tr이 작을수록 비교 대상 데이터가 줄어들어 처리 속도가 빨라졌다. 이러한 특성은 Yoshizawa, Takasaki와 Ohmura (2013)이 가속도 기반 동작 인식 시스템에서 윈도우 크기, 필터 수 등 파라미터 설정을 통해 연산량과 응답 시간 간의 상관 관계를 정량적으로 규명한 결과와도 부합한다.
결과적으로 n_tr=400, dt_tr=0.002, T_samp=0.2의 조건에서도 시험 데이터 형성에는 평균 0.026초, 동작 식별에는 평균 0.611초가 소요되어 총 평균 0.637초로, 1초 이내에 실시간 동작 인식이 가능함을 확인하였다. 이는 시스템의 주요 파라미터가 데이터 처리 속도와 직결됨을 보여주며, 실시간성 확보를 위해 최적의 샘플 길이와 학습 데이터 개수 설정이 필수적임을 시사한다.
이 때의 시험 데이터 형성 시간은 윈도우 분할, 특징 추출 및 정규화 과정까지 포함된 시간으로 실제 환경에 적용할 시 시험 대상자의 신체 사이즈 측정을 제외하면 레이더 신호 측정 이후 하나의 동작이 어떤 동작인지 식별되는데 소요되는 총 시간을 의미한다. 이는 실제 실시간 환경에서도 동일한 프로세스가 시간 제약 내 수행될 수 있음을 보여주지만 향후 각 단계별 지연 시간 분석을 통해 실시간 처리 능력을 더욱 신뢰성 있게 검증할 필요가 있을 것으로 판단된다.
본 연구에서는 레이더 기반 동작 인식을 위한 최적의 다운 샘플링 및 시간 분할 파라미터를 도출하였다. 다운 샘플링 조건에서는 d_samp=5, ds_ratio=16이 가장 우수한 성능을 나타냈으며, 시간 분할 조건에서는 T_samp=0.6일 때 충분한 샘플링 길이를 확보하여 동작의 주기적 패턴을 포괄할 수 있었으며, 이때 dt_tr의 변화는 학습 데이터 개수인 n_tr에만 영향을 미쳤고, n_tr은 정확도에 큰 영향을 미치지 않는 것으로 해석된다. 그럼에도 불구하고 본 연구에서는 T_samp=0.6 조건에서 dt_tr 변화에 따른 데이터 간 분산을 정량적으로 파악하여 최적 조건을 설정하고자 하였으며, 그 결과 CV=2.34%로 가장 낮은 값을 나타낸 dt_tr=0.004를 최적의 조건으로 선정하였다.
도출된 최적 파라미터에 대해 다양한 잡음 환경에서의 성능을 확인하기 위해 가우시안 백색 잡음을 추가한 실험을 수행하였다. <Figure 10>의 결과에 따르면, SNR=0 dB 조건에서는 정확도가 79.28%로 낮아졌지만, SNR=5 dB 이상의 환경에서는 90% 이상의 정확도를 유지하는 것으로 나타났다. 기존 연구에서도 90% 이상의 정확도를 달성한 인식 시스템은 실제 환경에서 활용 가능한 견고한 성능(robust perform- ance)으로 평가되고 있다(Ding et al., 2022). 따라서 본 연구에서 제안한 파라미터 조합은 시간 · 거리 축 해상도와 데이터 처리 효율성 간의 균형을 고려해 설계되었으며, 다양한 잡음 환경에서도 안정적으로 동작 인식 성능을 유지함으로써 실질적인 현장 적용 가능성을 입증하였다.
이상의 결과는 단일 FMCW 레이더를 활용한 다중 대상자 동작 인식 시스템이 실제 환경에서도 실시간으로 작동 가능한 수준의 정확도와 처리 속도를 달성할 수 있음을 보여준다. 특히 다운 샘플링 및 시간 분할 최적화 전략은 복잡한 환경에서도 신호 손실을 최소화하면서 시스템의 효율성을 높이는 데 효과적임을 입증하였다.
본 연구는 레이더 기반 동작 분석 기술을 실질적인 스포츠 현장이나 재활, 생활 모니터링 분야에 적용할 수 있는 가능성을 제시하며, 기존의 광학 기반 시스템이 가지는 설치 제약 및 피검자 간섭 문제를 해결할 수 있는 대안으로 기여할 수 있다. 그러나 본 연구에서 제안한 FMCW 레이더 기반 기법은 동작의 분류 및 인식에는 높은 정확도를 보였으나, 스포츠 과학이나 생체역학 분야에서 필수적으로 요구되는 관절 위치나 관절 각도와 같은 정량적 움직임 지표를 직접적으로 산출하는 데에는 기술적 한계가 존재한다. 따라서 본 연구에서 제안한 방식은 고가의 마커 기반 광학식 모션 캡처 시스템을 완전히 대체하기보다는, 간편하고 비용 효율적인 모니터링 도구로서 보완적으로 활용될 수 있는 가능성을 보여주는 탐색적 시도로 이해되어야 한다.
또한, 본 연구는 마커 부착 없이 레이더 신호만으로 동작 인식을 구현하는 것을 목표로 하고 있지만, 실제 실험에서는 시험 대상자의 마커 데이터를 활용해 시뮬레이션 신호를 생성한 점에서 마커리스 시스템이라는 주장과 완전히 일치하지 않을 수 있다. 다만, 시험 대상자의 신체 각 분절의 길이를 사전에 파악할 수 있다면, 학습 데이터로 사용된 마커 위치 데이터의 크기를 시험 대상자의 신체 크기로 보정하여 인식에 활용할 수 있을 것으로 판단된다. 이는 향후 완전한 마커리스 시스템 구현을 위한 기반 기술로 발전시킬 수 있을 것이다.
본 연구는 한 명의 대상자 데이터를 기반으로 학습 데이터를 생성하였기 때문에, 동일한 동작이라도 대상자의 체형과 운동 스타일에 따라 신호 패턴이 미세하게 달라질 수 있다. 따라서 동일 동작에서도 다양한 패턴의 신호를 포함한 학습 데이터를 확보한다면, 모델의 편향성을 줄이고 보다 강인한 동작 인식 성능을 달성할 수 있을 것으로 판단된다. 이를 위해 향후 연구에서는 복수의 학습 데이터를 활용하는 방안이 필요하다.
또한 본 연구에서 평가된 동작들은 대부분 시상면에서 일어나는 평면적 움직임에 국한되어 있으며, 고관절이나 어깨 관절의 축 회전과 같은 복합적인 3차원 움직임은 포함하지 않았다. 현재의 레이더 신호가 이러한 비평면적 · 회전 중심의 움직임에 대해 충분한 분해능과 구분 능력을 제공할 수 있는지는 아직 검증되지 않았으며, 이는 본 방법론의 적용 범위를 제한할 수 있는 중요한 한계점이다. 따라서 향후 연구에서는 다양한 움직임 방향성과 관절 수준의 복잡한 3차원 동작을 포함한 추가 검증이 필요하며, 이를 통해 본 기법의 활용 가능 범위를 보다 확장할 수 있을 것이다.
더불어 본 연구는 제한된 수의 실험 대상자와 특정 환경 내에서만 수행되었기 때문에, 다양한 연령층 · 체형 · 복장 조건에서의 일반화 가능성은 추가적으로 검증되어야 한다. 또한, 본 연구에서는 조건별 정확도의 차이를 기술통계적으로만 비교하였으며, 추리통계적 유의성 검정은 수행하지 않았기 때문에 결과 해석에는 이 점을 고려할 필요가 있다. 실제 다중 동작이 연속적으로 발생하는 상황에서의 인식 정확도와 처리 지연에 대한 분석도 향후 과제로 남아 있다.
본 연구는 광학 센서 기반 동작 분석 시스템의 제약을 극복하고자, 단일 FMCW 레이더를 활용한 다중 대상자 동작 인식 기법을 제안하였다. 제안된 기법은 고해상도 77 GHz FMCW 레이더 신호와 한 명의 대상자로부터 획득한 반사 마커 위치 데이터를 기반으로 한다. 해당 데이터로부터 상호 상관 기법을 활용하여 특성 벡터를 형성하고, 신호의 다운 샘플링 및 시간 분할 조건을 최적화함으로써 학습 및 식별에 소요되는 시간을 최소화하면서도 높은 인식 정확도를 유지할 수 있도록 설계되었다.
실험 결과, 최적 파라미터 조건(d_samp=5,ds_ratio=16,T_samp=0.6,dt_tr=0.004)에서는 95% 이상의 정확도를 달성하였으며, SNR=5 dB 이상의 잡음 환경에서도 90% 이상의 성능을 유지하여 시스템의 견고성을 입증하였다. 또한, 하나의 학습 데이터만으로도 다중 대상자의 동작 인식이 가능함을 확인하였으나, 이는 동일한 신체 조건을 가진 대상자가 아닌 상황에서 성능의 안정성을 완전히 보장하는 것은 아니므로, 범용성을 입증하기 위한 탐색적 시도로 해석되어야 한다. 시험 대상자 간 신체 조건과 특성 차이가 인식 성능에 미치는 영향을 체계적으로 분석하지 않았다는 점은 본 연구의 한계점으로, 향후 연구에서는 다양한 연령, 체형, 복장 조건을 고려한 후속 실험을 통해 일반화 가능성을 보다 정량적으로 검증할 필요가 있다.
본 연구의 기법은 향후 스포츠 훈련, 실내 모니터링, 재활 분야 등 다양한 실제 환경에 적용될 수 있을 것으로 기대되며, 향후 연구에서는 다양한 동작 유형과 복잡한 환경에서의 확장성과 실시간 처리 효율성을 더욱 향상시키는 방향으로 발전시킬 수 있을 것이다.
References
1. Arzehgar, A., Seyedhasani, S. N., Ahmadi, F. B., Bagheri Baravati, F., Sadeghi Hesar, A., Kachooei, A. R. & Aalaei, S. (2025). Sensor-based technologies for motion analysis in sports injuries: a scoping review. BMC Sports Science, Medicine and Rehabilitation, 17(1), 15.
Google Scholar
2. Chen, V. C., Li, F., Ho, S. & Wechsler, H. (2006). Micro-Doppler effect in radar: phenomenon, model, and simulation study. IEEE Transactions on Aerospace and Electronic Systems, 42(1), 2-21.
Google Scholar
3. Danzer, A., Griebel, T., Bach, M. & Dietmayer, K. (2019). 2d car detection in radar data with pointnets. Paper presented at the 2019 IEEE Intelligent Transportation Systems Con- ference (ITSC), 61-66.
Google Scholar
4. Das, K., de Paula Oliveira, T. & Newell, J. (2023). Comparison of markerless and marker-based motion capture systems using 95% functional limits of agreement in a linear mixed-effects modelling framework. Scientific Reports, 13(1), 22880.
Google Scholar
5. de Almeida, I. D. P., Corriça, J. V. D. P., Costa, A. P. D. A., Costa, I. P. D. A., Maêda, S. M. D. N., Gomes, C. F. S. & dos Santos, M. (2020, December). Study of the location of a second fleet for the Brazilian Navy: Structuring and mathematical modeling using SAPEVO-M and VIKOR methods. In International Conference of Production Research-Americas (pp. 113-124). Cham: Springer International Publishing.
6. Ding, C., Zhang, L., Chen, H., Hong, H., Zhu, X. & Li, C. (2022). Human motion recognition with spatial-temporal-convLSTM network using dynamic range-doppler frames based on portable FMCW radar. IEEE Transactions on Microwave Theory and Techniques, 70(11), 5029-5038.
Google Scholar
7. Eom, C. H., Chun, S. B., Kim, B. S., Joo, S. Y., You, J. H., Yoon, J. S., Han, S. J., Park, J. C. & Park, S. H. (2024). Simulation study for the motion classification using the radar and the 3D motion analysis system. Korean Journal of Applied Biomechanics, 34(4), 240-250.
Google Scholar
8. Eom, C., Han, S., Chun, S., Joo, S., Yoon, J., Kim, M., Park, J. & Park, S. (2025). Efficient markerless motion classification using radar. Sensors (Basel, Switzerland), 25(11), 3293.
Google Scholar
9. Hadjipanayi, C., Yin, M., Bannon, A., Rapeaux, A., Banger, M., Haar, S., Lande, T. S., McGregor, A. H. & Constandinou, T. G. (2024). Remote gait analysis using ultra-wideband radar technology based on joint range-doppler-time represen- tation. IEEE Transactions on Biomedical Engineering.
Google Scholar
10. Horiuchi, R., Hoshino, T., Oishi, N. & Suwa, K. (2021). Azimuth ambiguity discrimination using doppler spectrum of the compressive sensing-based SAR image with downsampled PRF. Paper presented at the 2020 17th European Radar Conference (EuRAD), 318-321.
Google Scholar
11. Kalyanaraman, A., Hong, D., Soltanaghaei, E. & Whitehouse, K. (2017). Forma track: tracking people based on body shape. Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies, 1(3), 1-21.
Google Scholar
12. Karatzas, N., Abdelnour, P., Corban, J. P. A. H., Zhao, K. Y., Veilleux, L., Bergeron, S. G., Fevens, T., Rivaz, H., Babouras, A. & Martineau, P. A. (2024). Comparing a portable motion analysis system against the gold standard for potential anterior cruciate ligament injury prevention and screening. Sensors, 24(6), 1970.
Google Scholar
13. Kim, S., Lee, S., Zhang, Y., Park, S. & Gu, J. (2023). Carbon-based radar absorbing materials toward stealth technologies. Advanced Science, 10(32), 2303104.
Google Scholar
14. LaHaie, I. J. (2003). Overview of an image-based technique for predicting far-field radar cross section from near-field measurements. IEEE Antennas and Propagation Magazine, 45(6), 159-169.
Google Scholar
15. Liu, J., Wang, L. & Zhou, H. (2021). The application of human-computer interaction technology fused with artificial in- telligence in sports moving target detection education for college athlete. Frontiers in Psychology, 12, 677590.
Google Scholar
16. Liu, Q., Zhang, X. & Liu, Y. (2024). SCNet: Scattering center neural network for radar target recognition with incom- plete target-aspects. Signal Processing, 219, 109409.
Google Scholar
17. Long, T., Zeng, T., Hu, C., Dong, X., Chen, L., Liu, Q., Xie, Y., Ding, Z., Li, Y. & Wang, Y. (2019). High resolution radar real-time signal and information processing. China Communications, 16(2), 105-133.
Google Scholar
18. Ma, X., Zhao, R., Liu, X., Kuang, H. & Al-Qaness, M. A. (2019). Classification of human motions using micro-doppler radar in the environments with micro-motion interference. Sensors, 19(11), 2598.
Google Scholar
19. Penichet-Tomas, A. (2024). Applied biomechanics in sports performance, injury prevention, and rehabilitation. Applied Sciences, 14(24), 11623.
Google Scholar
20. Piotrowsky, L., Jaeschke, T., Kueppers, S., Siska, J. & Pohl, N. (2019). Enabling high accuracy distance measurements with FMCW radar sensors. IEEE Transactions on Microwave Theory and Techniques, 67(12), 5360-5371.
Google Scholar
21. Seifert, A., Grimmer, M. & Zoubir, A. M. (2020). Doppler radar for the extraction of biomechanical parameters in gait analysis. IEEE Journal of Biomedical and Health Informatics, 25(2), 547-558.
Google Scholar
22. Sheeny, M., De Pellegrin, E., Mukherjee, S., Ahrabian, A., Wang, S. & Wallace, A. (2021). Radiate: A radar dataset for auto- motive perception in bad weather. Paper presented at the 2021 IEEE International Conference on Robotics and Automation (ICRA), 1-7.
Google Scholar
23. Song, K., Hullfish, T. J., Silva, R. S., Silbernagel, K. G. & Baxter, J. R. (2023). Markerless motion capture estimates of lower extremity kinematics and kinetics are comparable to marker-based across 8 movements. Journal of Bio- mechanics, 157, 111751.
Google Scholar
24. Stump, D. (2014). MTF, Resolution, Contrast, and Nyquist Theory. Digital Cinematography (pp. 111-126). Routledge.
Google Scholar
25. Tian, X., Bai, X. & Zhou, F. (2023). Recognition of micro-motion space targets based on attention-augmented cross-modal feature fusion recognition network. IEEE Transactions on Geoscience and Remote Sensing, 61, 1-9.
Google Scholar
26. Unger, T., de Sousa Ribeiro, R., Mokni, M., Weikert, T., Pohl, J., Schwarz, A., Held, J., Sauerzopf, L., Kühnis, B. & Gavagnin, E. (2024). Upper limb movement quality measures: com- paring IMUs and optical motion capture in stroke patients performing a drinking task. Frontiers in Digital Health, 6, 1359776.
Google Scholar
27. Van Der Donckt, J., Van Der Donckt, J. & Van Hoecke, S. (2025). tsdownsample: High-performance time series downsam- pling for scalable visualization. SoftwareX, 29, 102045.
Google Scholar
28. Van der Kruk, E. & Reijne, M. M. (2018). Accuracy of human motion capture systems for sport applications; state-of-the-art review. European Journal of Sport Science, 18(6), 806-819.
Google Scholar
29. Vasconcelos, M. J. M. & Tavares, J. M. R. (2008). Human motion analysis: methodologies and applications. Cmbbe 2008,
Google Scholar
30. Wang, T. (2024). Intelligent long jump evaluation system in- tegrating blazepose human pose assessment algorithm in higher education sports teaching. Systems and Soft Computing, 6, 200130.
Google Scholar
31. Yahya, M., Shah, J. A., Kadir, K. A., Yusof, Z. M., Khan, S. & Warsi, A. (2019). Motion capture sensing techniques used in human upper limb motion: A review. Sensor Review, 39(4), 504-511.
Google Scholar
32. Yoshizawa, M., Takasaki, W. & Ohmura, R. (2013). Parameter exploration for response time reduction in accelerometer-based activity recognition. Paper presented at the Pro- ceedings of the 2013 ACM Conference on Pervasive and Ubiquitous Computing Adjunct Publication, 653-664.
Google Scholar
33. Yuhai, O., Choi, A., Cho, Y., Kim, H. & Mun, J. H. (2024). Deep-learning-based recovery of missing optical marker trajec- tories in 3D motion capture systems. Bioengineering, 11(6), 560.
Google Scholar
34. Zuo, X., Tang, X. & Zhou, Y. (2020). Influence of sampling length on estimated fractal dimension of surface profile. Chaos, Solitons & Fractals, 135, 109755.
Google Scholar