동작분석은 인간의 자세를 평가하기 위해 특정 장비를 활용하여 움직임을 분석하는 것을 의미하며(Poppe, 2007), 이를 통해 인체 움직임에서 나타나는 운동학적 데이터를 수집할 수 있다. 이러한 동작분석은 임상 분야(Bleser et al., 2017)나 스포츠 현장의 경기력 향상(Salim, Lim, Salim & Baharuddin, 2010)을 위해 주로 사용된다. 동작분석에는 한 방향에서 데이터를 수집할 수 있는 2차원 분석과 3축에서 더 많은 정보의 데이터를 수집할 수 있는 3차원 분석이 있다. 현재 가장 널리 활용되는 3차원 동작분석 방식은 인체에 반사마커를 부착한 후, 광학센서 카메라를 통해 반사마커의 위치 좌표 데이터를 획득하여 인체를 모델링 하는 방식이다(Ganguly, Rashidi & Mombaur, 2021; Karatzas et al., 2024). 그러나 마커 기반 동작분석은 마커 부착과 데이터처리를 위한 시간, 카메라 설치 공간 등 시공간적 제약이 따른다. 또한 고가의 장비이며 반사마커 부착으로 인한 자연스러운 움직임을 방해할 수 있다는 단점이 있다(Das, de Paula Oliveira & Newell, 2023; Pagnon, Domalain & Reveret, 2021). 이러한 문제를 해결하기 위해 마커를 부착하지 않는 마커리스(markerless) 동작분석에 대한 연구가 활발히 진행되고 있고, 실제로 이를 활용한 동작 식별 알고리즘은 낙상을 감지하는 분석 방법으로 사용되고 있다(Kim, Yu & Xiong, 2024). 하지만 카메라를 활용한 동작 식별 시스템은 촬영된 영상을 사용하기 때문에 개인정보 보안에 취약하다는 한계점이 있다(Seifert, Grimmer & Zoubir, 2020).

반면 레이더 센서는 전자기 에너지를 방출하여 표적을 통해 반사되는 신호를 감지하는 방식으로 피사체의 형상을 획득하기 때문에(de Almeida et al., 2020), 개인정보를 보호하는 데 자유롭다고 할 수 있다. 또한, 해당 센서의 전자기 에너지는 빛의 속도로 방출되기 때문에 물체와의 거리, 속도, 위치 등을 정밀하게 측정할 수 있으며(Kim, Lee, Zhang, Park & Gu, 2023), 이는 최근 동작분석에서 활용되고 있는 저렴한 카메라와 비교하여도 가격대비 우수한 성능을 보여준다. 높은 정확도를 보이는 고가의 광학센서 카메라 기반 동작분석 장비와 비교한다면 저렴하고 크기가 작아 설치가 간편하며 대상자의 인체에 센서를 부착하지 않아 자연스러운 움직임을 유도할 수 있을 뿐만 아니라, 보다 짧은 시간을 할애하여 자료를 수집할 수 있다는 이점이 있다. 또한 레이다(radar)는 광학센서와 달리 넓은 지역을 탐지할 수 있고(LaHaie, 2003), 날씨 및 주야와 관계없이 정확한 정보를 제공할 수 있으며(Sheeny et al., 2021), 광대역 신호를 통해 고해상도로 물체를 감지하고 추적할 수 있다. 이러한 장점으로 인하여 현재 다양한 분야에서 레이다가 활용되고 있다(Danzer, Griebel, Bach & Dietmayer, 2019).

레이다는 반사 신호의 시간지연을 활용하여 표적까지의 거리를 추정할 수 있으며(Godrich, Haimovich & Blum, 2010), 도플러(doppler) 주파수 변조를 활용하여 이동하는 표적의 속도를 추정할 수 있다(Kellner, Barjenbruch, Dietmayer, Klappstein & Dickmann, 2013). 현재 레이다 분야 중 활발히 연구되는 분야는 미세도플러(micro-doppler, MD) 신호 분석이다. 이는 Chen, Li, Ho와 Wechsler (2006)에 의해 제안된 개념으로 표적의 도플러 주파수에 미세한 떨림 및 이동에 의한 시간 변동(time-varying) 도플러 효과를 포함한다(Lu, Kou & Wang, 2023). MD 신호는 Short-Time Fourier Transform (STFT)을 이용하여 레이다의 시선(line of sight, LOS) 방향에 대해 시간-주파수(time-frequency, TF) 영역에서 표적의 각 부분의 속도 변화를 2차원 영상으로 나타내며, 이를 통해 표적의 미세 운동을 시각적으로 표현할 수 있다(Qian, 2002). 그러나 이러한 MD 영상을 분석하여 표적을 식별하는 과정은 매우 복잡하며, 여러 특성을 추출한 후 이를 벡터로 구성하여 식별하는 방식이 사용된다. 이는 표적에 따른 효과적인 특성을 추출함으로써 매우 작은 차원의 벡터를 활용하여 자동으로 식별이 가능하기 때문이다. 이러한 특성에는 MD 영상 내 미세 운동의 주기와 미세 운동 속도로 인한 대역폭 및 영상 내 산란원의 크기 등이 있을 수 있으며, 이외에도 다양한 형태의 표적에 따른 특성이 존재한다(Chen et al., 2006). 이처럼 인체의 동작 식별에서도 고해상도의 MD 영상과 적절한 특성 추출이 가능하다면, 전체 수신 신호와의 상호상관(cross-correlation)을 활용하여 매우 효과적인 특성벡터를 구성할 수 있고 이를 통해 효과적인 동작 식별이 이루어질 수 있다.

하지만 기존에 수행된 레이더를 활용한 움직임 식별연구들은 주로 금속체의 미세 운동을 식별하는 데 활용되었으며(Jian, Lu & Chen, 2017), 인간의 움직임을 식별하는 연구는 미비한 실정이다. 이는 레이더 센서를 활용하여 신체 움직임에 대한 레이다 반사 신호를 분석하는 데 있어 3차원 운동을 정확하게 모델링 하기 위한 복잡한 수식이 필요하며(He et al., 2015), 전자기파의 반사 특성에 따른 변화를 예측하기 어렵다는 제한점이 있다(Sengupta, Jin, Zhang & Cao, 2020). 따라서, 레이다를 활용한 효과적인 동작 식별 방법을 고안하기에 앞서 레이다 신호 모델링, MD 영상 형성, 그리고 효과적인 특성 추출을 위한 연구가 필수적이라고 할 수 있다. 본 연구에서는 광학센서 카메라로 측정한 마커의 3D 위치 데이터를 활용하여 레이다 신호를 구성한 후, 정확한 3차원 레이다 신호 모델링을 통해 전체 레이다 수신 신호를 구성하고자 한다. 또한 모델링 된 신호를 통해 TF 영상 특징을 분석하는 방법 및 효과적인 특징 추출 방법을 제안하고자 한다.

1. 대상자

본 연구는 6개월 이내 상/하지에 부상 경험이 없는 성인 남성 2명, 여성 3명을 대상자로 선정하였다. 모든 연구 대상자는 연구 목적, 실험 절차 및 주의 사항을 설명한 후, 실험 참여에 동의한 대상자에 한해 자료 수집을 진행하였다. 본 연구는 본교 생명윤리위원회로부터 승인을 받았으며(IRB 승인번호: 1041386-202407-HR-96-02), 모든 참가자로부터 자발적으로 참여한다는 서면 동의서를 받았다. 연구 대상자의 특성은 <Table 1>과 같다.

2. 실험장비

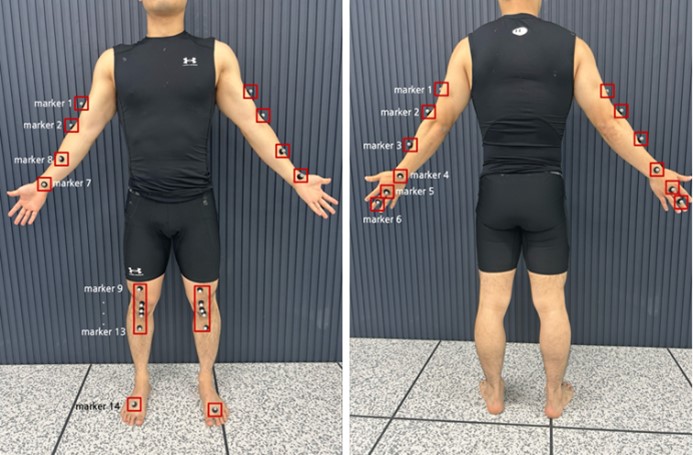
마커의 위치데이터를 획득하기 위해 8대의 광학 모션 캡처 카메라(Miqus M5; Qualisys AB, Gothenburg, Sweden; sampling rate 250 Hz)를 사용하였고, 3차원 공간 좌표화를 위해 NLT (non-linear transformation) 방식의 캘리브레이션(calibration)을 진행하였다. 이때 좌우 방향을 x 축, 전후 방향을 y 축, 수직 방향을 z 축으로 정의하였다. 반사마커는 12 mm의 크기를 사용하였으며, 부착 위치는 <Figure 1>에 표시된 28곳 중 전후 움직임이 크게 형성되는 양 측 부위에 각 5개씩 총 10개를 부착하였다(Table 3). 마커 부착 위치의 해부학적 위치는 <Table 2>와 같다. 또한 반사마커의 위치데이터는 QTM (Qualisys Track Manager; Qualisys, Gothenburg, Sweden) 프로그램을 사용하여 획득하였다.

Figure 1. Marker positions.

Modify Delete

3. 측정

모든 대상자는 본인의 신체 크기에 맞는 준비된 스판덱스 소재의 실험복으로 환복한 뒤, 부상 방지를 위해 10분 간의 준비 운동을 수행하였다. 수행 동작의 경우 MD 신호가 측정 대상의 거리를 측정하는 것이 아닌 거리의 변화를 측정하는 값이기 때문에 전후로 움직임이 많은 웨이트 트레이닝을 대표하는 총 5가지의 동작을 선정하였으며 하지 움직임의 스쿼트(squat), 런지(lunge), 양발 번갈아 앞차기(front kick) 동작과 상지 움직임의 프론트 레터럴 레이즈(front lateral raise), 덤벨 컬(dumbel curl) 동작을 수행하였다(Figure 2). 이때 한 동작 당 60 BPM (beat per minutes)에 맞춰 회당 2초씩 2회 반복하여 총 4초간 수행하였다.

Figure 2. Motion for measurement. (A) squat, (B) lunge, (C) front kick, (D) front lateral raise, (E) arm curl

Modify Delete

4. 신호 모델링, 미세도플러 이론 및 신호 분류 방법

마커의 위치데이터는 추후 실제 레이더 측정을 활용한 동작분석 알고리즘 개발을 위해 필터링 없이 기존 데이터를 사용하여 신호를 추출하였다. 수집된 자료는 QTM 프로그램을 통해 mat 파일로 변환하였으며, 마커의 위치데이터를 활용하여 레이다 신호를 모델링하기 위해 MATLAB R2023b (MATLAB; MathWorks, Natick, Massachusetts, USA)을 사용하였다.

1) 마커 좌표를 사용한 레이더 신호 모델링

레이다 신호의 경우, 연속파(continuous wave, CW) 신호를 사용한다. CW 레이다는 기본적으로 시간(timing)이 제공되지 않으므로 거리를 측정할 수 없으나, 시간에 따른 도플러 주파수 변조를 제공한다. 시간 t에서 주파수 f0로 송신된 복소 CW 전자기파 신호 s(t)는 다음 식과 같다.

위 식에서 이다. 이 신호가 거리 r(t)에 위치한 산란원에서 반사될 경우, 수신된 신호 는 다음과 같이 시간 지연이 발생하게 된다.

위 식에서 c는 공기 중에서 전자기파의 속도이며, 빛의 속도 = 3 x 10^8 m/s와 동일하다. 식 (2)의 경우 매우 높은 주파수에서 진동하므로, MD를 추출하기 위해서 다음과 같이 기저대역으로 하향 변환하였다.

위 식에서 는 동작 주파수에서의 파장이다.

다수의 산란점이 존재할 경우, 수신된 기저대역 신호는 다음과 같이 각 산란원으로부터 반사된 신호의 합으로 표현할 수 있다(Cha, Park, Kim & Choi, 2021).

위 식에서 는 표적 내 산란점의 크기이며, 는 k번째 산란원과 표적과의 거리이다. 전자기적인 평면파 특성에 따라 는 표적의 3차원 좌표가 LOS 방향으로 투영된 거리이다. 본 논문에서는 이러한 를 마커 좌표를 이용하여 모델링 하였다.

2) 미세도플러

식 (4)의 k번째 산란원의 위상성분 를 식 (5)와 같이 표현할 수 있으며, 이를 시간에 따라 미분하기 위해 식 (6)과 같이 이 산란원의 시간 변동 MD 신호 를 추출하였다.

이를 이용하여 전체 MD 신호는 다음과 같이 각 산란원 MD의 합으로 표현할 수 있다.

식 (7)의 MD를 고속 푸리에 변환(fast fourier transform, FFT)할 경우, 전체적인 스펙트럼으로 표현되어 시간에 따른 주파수 변화를 확인할 수 없다. 따라서 본 연구에서는 TF 영역에서 를 표현하였다. TF 영상에서 사용되는 기법 중 가장 많이 사용되는 기법은 STFT이다. STFT 기법의 경우, TF 영상을 분석하는 기법 중 가장 간단한 방법이며 <Figure 3>과 같이 주어진 시간 t 주변의 윈도우(window) w(t) 이내의 데이터를 FFT 하여 얻은 주파수 스펙트럼을 모든 시간의 세로 방향에 대하여 순차적으로 수표시하는 방법이다. 수학적으로는 다음과 같이 표현할 수 있다.

Figure 3. STFT (Qian, 2002).

Modify Delete

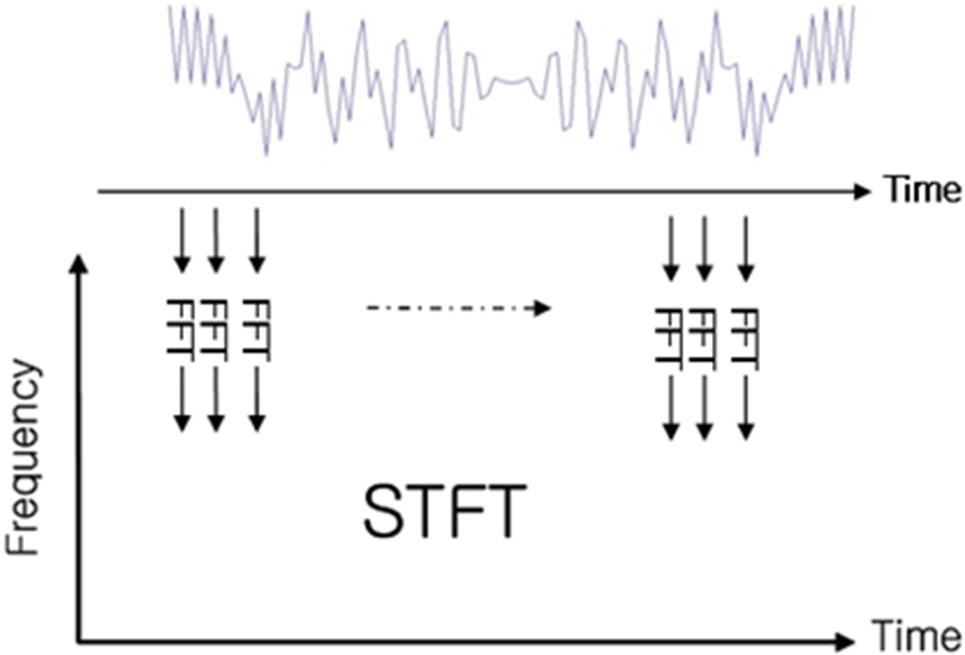
이러한 STFT 후, 각 산란원의 MD가 TF 영역에 표현될 수 있다. 본 연구에서 w(t)는 단순한 사각 윈도우를 사용하였다.

3) 특성벡터를 사용한 학습 데이터 구축

학습데이터 구성 시에는 통상적인 레이다 표적 식별 분야에서 사용되는 기법을 활용하였다(Kim, Seo & Kim, 2002). 우선, 각 동작 별로 식 (4)에 따라 구성된 레이다 수신 신호를 균일한 간격으로 잘라내서 TF 영역데이터를 형성하였으며, <Figure 4>와 같이 동작 별로 형성된 0 ~ 길이의 전체 시간영역 신호에서 균일한 간격 로 길이 의 신호를 추출하였다. 따라서 표적 별 학습 TF 영상은 총 개이다. 각각 추출된 길이 의 신호를 이용하여 <Figure 3>의 STFT 영상을 형성할 때, 동일한 간격으로 순차적으로 잘라낸 후 이를 FFT 하여 쌓는 방식으로 TF 영상을 형성하였다.

Figure 4. Construction of the training data sampled at uniform time interval.

Modify Delete

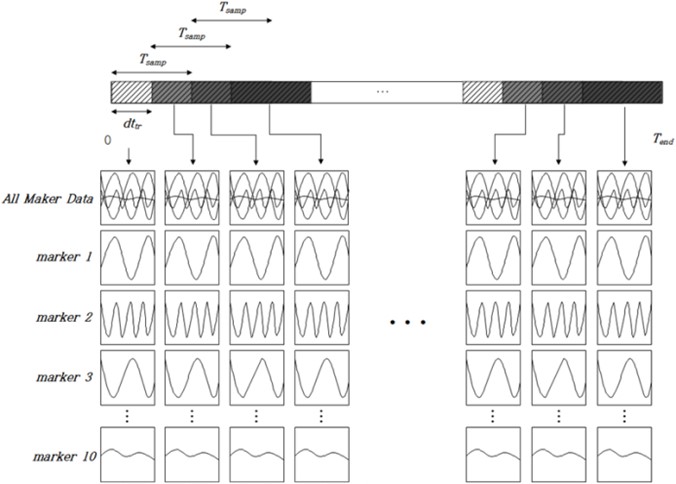
본 연구에서는 전체 마커 신호를 중첩하여 형성된 TF 영상을 실제 측정된 영상으로 가정하였으며, 각 마커의 TF 영상을 미리 알고 있는 마커 정보로 가정하였다. 즉, 마커 개수를 식 (4)의 로 가정할 경우, 개의 마커 TF 영상의 합이 측정된 신호이며, 각 마커의 TF 영상이 미리 알려진 특징 추출을 위한 영상이다. 특징의 경우, 다음 식과 같이 학습영상 내 각 마커 TF 영상과의 최대상호상관(maximum cross-correlation)을 적용한다. 정규화된 전체 마커 TF 영상을 이라고 가정하고, k번째 마커의 TF 영상을 로 가정할 경우, 상호상관은 다음과 같다.

위 식에서 p와 q는 영상의 행 및 열 방향 원형이동(circular shift)이며, 및 는 식 (10)과 같은 방식으로 거리에 상관없이 최대 상관 값이 1이 되도록 정규화 한 영상이다.

모든 이동에 대해서 식 (8)을 적용할 경우는 매우 많은 시간이 필요하므로, 본 연구에서는 FFT의 주파수 특성을 활용하여 다음과 같이 계산하였다.

위 식에서 FFT2와 IFFT2는 2차원의 FFT와 역(inverse) FFT이다.

식 (9)을 이용하여 추출된 k번째 마커의 특징은 Cor의 최댓값이며, 다음과 같다.

만약 k번째 마커의 정보가 측정데이터에 포함될 경우, 는 크고 그렇지 않을 경우 값이 작다. 개의 마커를 이용하여 특성을 추출할 경우, 각 학습 TF 영상에 대한 특성벡터는 다음과 같이 구성된다.

최종적으로, 각 동작 별로 다음과 같은 학습 특성행렬이 구성된다.

위 식에서 는 표적 내 k번째 학습 특성벡터이다.

4) 신호 분류 방법

시험을 위한 데이터는 <Figure 4>의 신호 범위에서 랜덤하게 만큼 추출한 후 형성된 TF 영상을 사용하였다. 학습 특성벡터와 마찬가지로, 각 학습데이터의 마커 정보와의 최대 상호상관을 이용하여 시험벡터 를 구성한 후, 구분 시에는 식 (15)와 같이 특성벡터 간 유클리디안 거리를 가장 가까운 거리의 학습 특성벡터 를 가지는 동작을 시험벡터의 동작으로 구분한다. 유클리디안 거리는 다음과 같이 정의된다.

구분되지 않은 동작의 시험벡터가 이고, i번째 동작에 속하는 학습벡터가 일 때, 최종 동작은 다음과 같은 규칙에 의해서 결정된다.

5. 시험데이터와 학습데이터의 특징

본 연구에서 MATLAB 신호 모델링 시, 측정 대상자의 위치는 (0, 5, 0)으로 설정하였고 LOS는 (0, 1, 0)으로 설정하여 영상을 추출하였다. 레이다의 중심 주파수 = 24 GHz로 설정하였으며, 공기 중의 전자기파 속도 c를 고려하여 파장 λ = c/ = 0.0125 m이다. 주파수 영역의 중첩(aliasing)을 방지하기 위해 여러 측정을 통하여 최대 MD 크기 = 13/λ = 1.040 kHz로 설정하였으며, 에 따른 모델링 신호의 샘플링 간격 dt = 1/ /2 = 0.00048 sec로 설정하였다. 또한 이러한 dt에 맞게 동작 당 250 Hz로 샘플링한 마커 위치데이터를 1차원 보간(interpolation)을 통하여 샘플링 개수를 5,201개로 증가시켰다. STFT 시 주파수 영역 샘플을 위한 시간 윈도우 = 64 x dt = 0.0307 sec로 설정하였으며, 인접한 사이에 5개의 시간 샘플( = 5 x dt = 0.0024 sec)이 겹치도록 설정하였다(Table 4).

학습데이터 형성 시, 동작 당 전체 = 4 sec(5,201개 샘플) 중 = 0.8 sec(1,040개 샘플)을 활용하여 학습 TF 영상을 구성하였으며, 이를 = 0.015 sec(20개 샘플) 간격으로 반복하여 총 208개 TF 영상을 학습데이터로 구성하였다(Figure 4). 따라서 대상자 당 전체 학습 TF 영상 수는 1,040개이다. 해당 초기 설정 값은 다양한 실험 경험을 기반으로 하여 90% 이상의 구분율을 보이는 적절한 값으로 설정하였다. 시험데이터는 동작 당 0~4 sec 사이에서 랜덤하게 50개의 시작점을 선정한 후, 각 시작점에서 길이의 신호를 모델링하여 TF 영상을 형성하였다. 잡음의 영향을 분석하기 위하여 잡음이 없는 데이터의 구분율을 확인하였으며, 가산 백색 잡음(additive white Gaussian noise, AWGN)을 신호 대 잡음비(signal-to-noise-ratio, SNR) 0부터 20 dB까지 5 dB 간격으로 설정하여 구분율을 분석하였다(Tian, Bai & Zhou, 2023). 또한 학습데이터 구성에 사용되는 여러 변수 중 의 샘플링 간격을 0.015 sec(20개 샘플)부터 1.554 sec(2,020개 샘플)까지 0.385 sec(500개 샘플) 간격으로 설정하여 구분율을 분석하였고, 의 크기를 0.16 sec(전체의 4%)부터 0.8 sec(전체의 20%)까지 0.16 sec(전체의 4%) 간격으로 설정하여 구분율을 분석하였다.

1. 각 동작의 시간-주파수 분석

4 sec 간 측정한 각 동작의 TF 영상을 추출한 결과물은 <Figure 5>와 같다. 시간에 따라 각 동작의 고유 특성이 시간-주파수 영역에서 형성됨을 확인할 수 있다.

Figure 5. TF image of each motion. (A) squat, (B) lunge, (C) front kick, (D) front lateral raise, (E) arm curl are shown for each motion TF image.

Modify Delete

2. 노이즈가 없는 환경의 분류 결과

잡음이 없는 환경에서 대상자 Subject 1 - Subject 5의 동작구분 결과는 <Figure 6>와 같다. Subject 1, 2, 4는 100%, Subject 3은 96.8%, Subject 5는 99.2%로 나타났다.

Figure 6. Classification results (P_c) of the 5 subjects in noise-free environment.

Modify Delete

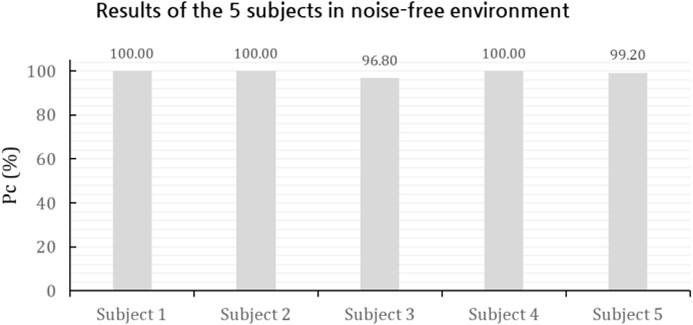
3. 노이즈와 좌표 오차의 영향에 대한 분류 결과

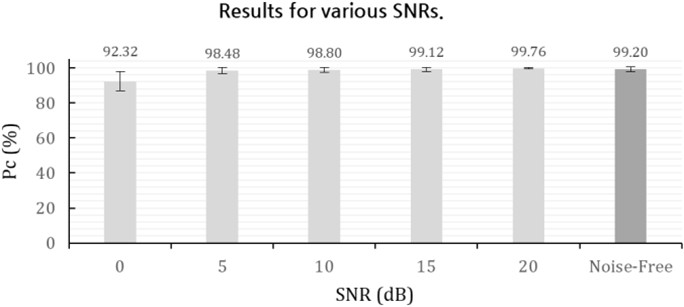
시험데이터에 0~20까지 5 dB 간격으로 SNR을 설정하여 구분 성능을 확인한 결과는 <Figure 7>과 같이 SNR = 20 dB에서 99.76%, SNR = 15 dB에서 99.12%, SNR = 10 dB에서 98.8%, SNR = 5 dB에서 98.48%, SNR = 0 dB에서 92.32%로 나타났다.

Figure 7. Classification results (Pc) for various SNRs.

Modify Delete

4. 학습 데이터의 매개변수 분석

잡음이 없는 상황에서 학습데이터 형성 시 사용되는 여러 변수의 영향에 대한 분석을 수행한 결과는 다음과 같다.

1) 학습데이터 의 영향에 대한 분류 결과

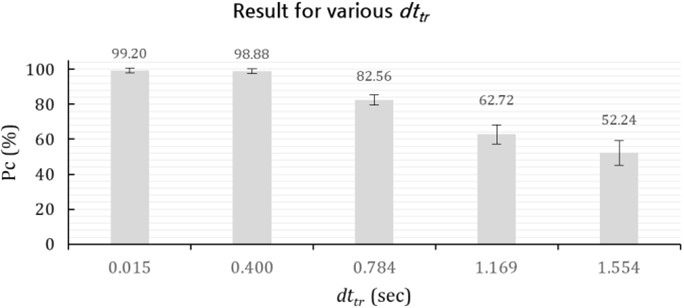
학습데이터 샘플링 간격이 구분결과에 미치는 영향을 분석하기 위하여 = 0.015 sec부터 0.385 sec 간격으로 1.554 sec까지 구분 실험을 수행하였으며, 그 결과는 <Figure 8>과 같다. 그림에서 보는 바와 같이, 이 0.015 sec일 때 99.2%, 0.400 sec일 때 98.88%, 0.784 sec일 때 82.56%, 1.169 sec일 때 62.72%, 1.554 sec일 때 52.24%로 나타났다.

Figure 8. Classification results (P_c) for various dt_{tr}s.

Modify Delete

2) 학습데이터 의 영향에 대한 분류 결과

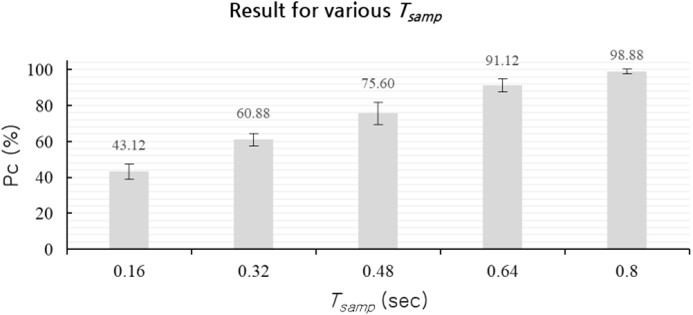
<Figure 8>의 실험 결과를 바탕으로 = 0.4 sec으로 설정한 후, 학습데이터 형성 시 TF의 시간 길이에 대한 영향을 분석하기 위하여 = 0.16 sec부터 0.16 sec 간격으로 0.8 sec까지 변화시키면서 구분 성능을 분석한 결과는 <Figure 9>과 같다. 자르는 구간이 0.8 sec일 때 98.88%, 0.64 sec일 때 91.12%, 0.48 sec일 때 75.6%, 0.32 sec일 때 60.88%, 0.16 sec일 때 43.12%로 나타났다.

Figure 9. Classification results (P_c) for various T_{samp}

Modify Delete

본 연구는 레이다의 동작 식별 가능성에 대해 파악하기 위해 3D 동작분석 시스템을 활용한 마커의 위치데이터를 기반으로 레이다 신호를 생성하여 적절한 특성을 확인하고자 하였다. 본 연구의 동작 별 TF 영상을 보면 수식을 사용하여 인간을 모델링한 후 동작을 TF 영상으로 표현한 Dirhold와 Ohtsuki (2012)의 연구와 같이 큰 움직임이 있는 부위에 대한 위치의 변화량에 따라 영상이 형성되었다. Squat 동작의 경우 LOS 방향의 수직 운동이 주성분을 이루므로 세로축(주파수축)으로 주파수 대역폭이 매우 작음을 확인할 수 있었다. 또한, lunge와 front kick은 다른 동작들에 비해 전후 움직임이 가장 크기 때문에 주파수 대역폭이 훨씬 크다는 것을 확인할 수 있었다. 특히, front kick의 경우 다른 동작들에 비해서 천천히 수행되었기 때문에 가로축(시간축)에서 반복되는 빈도가 낮음을 확인할 수 있었다. 또한 LOS 기준으로 산란점들이 중첩되는 정도에 따라 TF 영상 내 픽셀의 크기가 매우 다양하게 변함을 확인할 수 있었다.

이전 연구에서 레이다는 점프 스쿼트 시 굽이 다른 신발 두 켤레와 맨발로 총 세 개의 신발 유형에 따라 서로 다른 결과 값을 보여주었고, 이들을 구분한 결과 80% 이상의 구분율을 보여주었다. 그러나 해당 연구는 레이다 측정 결과만을 활용한 연구였으며, 동작의 식별에만 중점을 두었다. 본 연구는 현재 동작분석의 골드 스탠다드인 광학센서 카메라와 레이다를 비교함으로써 레이다의 동작 식별 성능을 검토하고자 하였다(Karatzas et al., 2024). 이에 적절한 특성벡터를 확인하고자 마커의 위치데이터를 활용하여 가상의 레이다를 생성한 후 학습데이터와 시험데이터를 형성하여 시뮬레이션 하였다. Kim 등 (2002)의 연구는 TF 영상을 통한 구분 기법을 활용하기 위해 학습데이터를 마커 별 위치데이터에 대한 TF 영상으로 가정하였으며, 시험데이터는 레이다 측정에 대한 TF 영상으로 가정하였다.

Khawar, Abdelhadi와 Clancy (2015)의 연구에서는 SNR에 따라 90% 이상의 구분율을 기준으로 평가하였다. 본 연구는 실제 시험데이터 형성 시 다양한 형태의 AWGN이 존재할 수 있으므로, SNR에 따라 원신호에 잡음을 첨가하여 구분 성능을 확인하였다. 결과는 신호와 잡음의 전력이 동일한 SNR = 0 dB에서도 92.32%의 높은 구분율을 얻을 수 있었고, 20 dB에서는 99.76%로 잡음이 없는 환경과 거의 동일한 구분율을 얻을 수 있었다. 따라서 제안된 기법은 잡음이 있는 환경에도 동작 식별이 가능함을 보여주었다.

학습데이터 형성 시, 샘플의 간격은 좁을수록 세밀한 구분이 가능하기 때문에 높은 구분율을 얻을 수 있다(O, Ki, Triolo, & Shin, 2023). 본 연구에서는 전체 시간에서 학습데이터를 형성을 위해 자른 시간의 간격 와 이 중 하나의 학습데이터 형성을 위한 샘플링 간격 에 따라 구분율을 확인하였고, 은 작아질수록 높은 구분율을 보여주었다. Han, Pan, Long, Liang과 Shan (2020)은 샘플링 간격이 길 경우 레이다가 추적하는데 오류를 발생시키거나 대상을 놓칠 수 있다고 하였으며, 반대로 너무 짧을 경우 빈번한 신호로 인해 레이다의 리소스가 낭비된다고 보고하였다. 본 연구에서도 마찬가지로 샘플링 간격이 커질수록 학습데이터 수의 저하로 구분율이 저하됨을 확인할 수 있었으며, 샘플링 간격을 줄일 경우 동작 당 생성되는 학습데이터의 양이 증가하여 구분에 필요한 소요시간 또한 증가하게 되는 것을 알 수 있다. 이는 높은 동작 식별에 대한 구분율을 확보하는 동시에, 메모리 공간 및 구분시간을 줄일 수 있는 적절한 이 매우 중요함을 시사한다. 반면 는 샘플링 간격의 길이가 짧아질수록 시간영역 특성부족으로 인하여 동작 식별에 대한 구분율이 저하되는 결과를 나타냈다. Kim, Paeng, Lee와 Lee (2014)는 데이터의 개수가 적어질수록 해당 데이터의 특성을 반영하지 못하기 때문에 인식률이 저하된다고 보고하였으며, 이는 TF 영역의 MD 영상에서 동작의 특성을 적절히 반영하기 위한 적당한 시간이 필요함을 시사한다.

본 연구에서는 등방성 산란점을 가정하여 각 동작 별 TF 영상을 추출할 수 있었으나, 실제 레이다 측정 시에는 산란원의 위치 변화, 주파수 및 각도에 따른 변화 등에 대해 추가적인 연구가 필요하다. 제안된 구분 기법을 활용한 결과, 잡음이 없는 상황에서 99.2%의 매우 높은 구분율을 달성하였고, 시험데이터의 잡음을 첨가한 구분율에도 높은 구분율을 보여줄 수 있었다. 그러나 잡음이 클수록 구분율이 감소함을 확인할 수 있었고, 이는 실제 레이다 측정에서 적절한 잡음처리가 필요하다는 것을 시사한다. 본 연구에서 제안된 기법은 매우 우수한 구분율을 보여주었으나, 간격을 좁게 설정하여 동작 당 208개의 매우 많은 학습데이터가 생성되었고, 이를 극복하기 위하여 간격을 넓혀 학습데이터 수를 줄일 경우, 데이터 수의 부족으로 인하여 구분 성능의 저하가 매우 크다는 것을 확인할 수 있었다. 또한 TF 영상을 형성하기 위한 시간 길이 가 구분율에 매우 높은 영향을 미침을 확인할 수 있었다.

최종적으로, 98% 이상의 성능을 나타낸 결과 값을 기존 분류 방법으로 대체할 수 있을 것이라 판단한 이전 연구를 바탕으로, 본 연구에서 >0.8 sec, <0.4 sec에서 98.8%의 구분율을 보였으므로 이러한 결과는 실제 레이더를 활용한 동작 인식에서 >0.8 sec, <0.4 sec의 설정 값을 참고한다면 뛰어난 성능의 동작 인식이 가능할 것으로 판단된다(Hong, Yi, Jo, Lee & Seo, 2019). 그러나 실제 환경은 알 수 없는 곳에서 첨가되는 잡음, 대상자의 신체 특성에 따른 산란점의 위치 등과 같이 시뮬레이션 환경에서 예상할 수 없는 기술적 과제가 있을 것으로 예상되며 이를 위해 추가적인 후속 연구가 진행될 필요가 있을 것으로 판단된다.

또한 더 나아가 레이더를 활용한 더욱 세밀한 동작분석을 위해서는 산란점의 정확한 위치를 추정할 수 있어야 한다. 현재 레이더 기술로는 관절의 위치벡터를 직접적으로 추정할 수 없으며, 인체를 투과하는 과정에서 반사되는 산란점의 위치를 정확히 추정하는 데에 어려움이 있다. 이러한 문제는 추후 선행연구를 바탕으로 인체의 산란점을 예측하는 모델을 개발하거나 레이더의 시선 개수를 늘리는 등 다양한 알고리즘 개발을 위한 추후 연구가 지속적으로 이루어져야 할 것이다(Chen, Guo & Wang, 2023; Dheenathayalan, Small, Schubert & Hanssen, 2016).

이와 같은 연구는 실질적인 레이더 기반 동작 인식 및 분석 기술의 발전에 중요한 기여를 할 것으로 사료된다.

본 연구에서는 실제 레이다를 이용하여 동작분석을 수행하기 위한 전 단계로, 3D 동작분석 시스템을 활용하여 얻은 마커 위치 좌표를 이용하여 수학적인 레이다 신호를 모델링 하였으며, 이를 통해 모델링 된 레이다 신호를 활용한 동작 식별의 효과적인 구분을 위한 적절한 특징을 다음과 같이 확인할 수 있었다. 본 연구를 통해 TF 영역에서 각 동작의 특성을 확인할 수 있었으며, 낮은 SNR에도 불구하고 제안된 기법의 우수성을 확인할 수 있었다. 또한 실제 인체 동작 식별에 사용되기 위해서 충분한 학습데이터 길이 >0.8 sec 및 충분한 샘플 간격 <0.4 sec가 필요함을 확인할 수 있었다.

본 논문은 광학식 카메라를 활용하여 측정된 마커 정보를 통해 모델링 된 레이다 신호와 이를 이용한 특성벡터 및 구분 기법에 대해 제안하였다. 본 연구에서 수행한 다양한 특성 값의 변화에 따른 결과를 통해, 제안된 기법이 모델링 된 신호에서 매우 효과적임을 알 수 있었다. 그러나, 2차원 영상을 통한 동작 구분은 많은 시간이 소요됨을 알 수 있었으며, 실제 레이다 신호의 경우 산란원의 위치 변화, 주파수 및 각도에 따른 변화 등 다양한 요인이 존재하기 때문에 추가적인 분석의 필요성을 알 수 있었다. 따라서, 후속 연구를 통해 TF 영상으로 변환하기 이전에 원신호를 활용하여 구분해야 하며, 5 GHz 이상의 대역 CW 레이다를 활용하여 다양한 비교 및 구분 실험이 수행돼야 할 필요성이 제기된다. 또한 레이다를 활용한 마커리스 동작 분석을 수행하기 위해, 동작 식별 알고리즘을 활용하여 레이다의 시선을 추가함으로써 레이다를 활용한 동작분석의 가능성을 높일 수 있을 것이다.