다중 손가락(multi-digit)을 사용하여 물체를 안정적으로 잡고 조작하는 쥐기(prehension)은 일상 생활에서 흔하게 요구되는 인간의 기능적 움직임이다. 잡은 물체를 평형(equilib- rium) 상태로 유지하기 위해서는 물체의 위치를 결정하는 손가락 합력(net force)과 방향(orientation)을 결정짓는 모멘트의 합(net moment)을 일정하게 유지해야 하며(Shim, Latash & Zatsiorsky, 2005a), 중추신경계(CNS)에 의해 개별 손가락에 가해지는 기계적 효과가 원활하게 조정되어야 한다. 중요한 점은, 특정 net force와 net moment를 만족하는 개별 손가락의 force와 moment의 조합은 무한하기 때문에 multi-digit pre- hension은 운동요소의 과잉(motor redundancy)이 내재된 전형적 특성을 지닌다(Park, Kim & Shim, 2010; Shim, Latash & Zatsiorsky, 2003, 2005b; Song, Kim, Ambike & Park, 2022). 이 운동요소의 과잉은 비단 prehension에서만 나타나는 특징이 아니라 인간의 모든 움직임, 모든 제어 계층(control hierarchy)에 존재하는 고유한 특성이다. 예를 들어, 팔을 뻗어 물체를 잡는 과제(arm reaching task)에서 어깨, 팔꿈치, 손목을 포함하는 상지 관절의 자유도는 물체의 위치를 규정하는 3차원 자유도를 초과하여 다양한 자세(configuration)로 동일한 과제 수행(i.e., 같은 위치의 물체를 잡는 동작)을 허용한다. 또한, 단일 관절의 토크 생성은 관절을 지나는 여러 근육 힘(muscle force)의 조합으로 달성되며, 단일 근육의 힘 조차도 여러 운동단위(motor unit)의 활성에 의해 조절되기 때문에 제어 체계 전반에 걸쳐 운동요소의 과잉을 확인할 수 있다. 따라서 CNS는 움직임을 안정화 하기 위해 과제 수행 동안 과잉된 자유도를 효율적으로 조직화 해야 하는 과잉의 문제(problem of motor redundancy)에 직면하게 된다(Latash, 2012, 2017).

CNS가 이 과잉의 문제를 어떻게 해결하는지에 대해 설명하는 여러 가설과 접근 방식이 제안되어 왔다. 일부 연구자들은 신경계가 최적화(optimization) 방식을 기반으로 유일한 최적의 단일 솔루션(optimal solution)을 찾는 방식으로 과잉의 문제를 해결할 수 있다고 주장했다(Todorov, 2004). 한편, 다른 연구자들은 풍요의 원리(principle of motor abundance)에 기초하여 운동요소의 과잉을 운동 제어에 대한 부담이나 해결해야 하는 문제로 여기지 않았다. 오히려 신경계는 과잉된 요소 변인의 차원에서 과제 수행을 안정화 할 수 있는 모든 솔루션 집합을 활용한다고 제안하였다(Latash, Scholz & Schoner, 2007; Song, Kim & Park, 2021). 이 과잉된 운동요소의 조직화를 통해 나타나는 과제 수행의 안정화를 시너지(motor synergy) 작용이라고 하며 비제어다양체(uncontrolled manifold, UCM) 분석을 통해 정량화 할 수 있다(Latash & Zatsiorsky, 2009; Scholz, Danion, Latash & Schoner, 2002; Scholz & Schoner, 1999; Song, Shin, Kim & Park, 2021). 이 시너지는 반복적인 인간 움직임에서 나타나는 동적 안정성(dynamic stability)의 지표로 활용되어 왔으며(Latash, 2020), 본 연구에서 다루는 중심 변인이 된다.

다섯 손가락을 이용한 prehension 제어는 Figure 1과 같이 두 제어 계층으로 구분된다. 직사각형 형태의 물체를 잡는 경우, 요구되는 기계적 효과는 상위 계층(upper hierarchy)에서 엄지 손가락(thumb)과 마주하는 네 손가락의 작용이 결합된 가상 손가락(virtual finger)으로 분배된다(Iberall, 1997; Zatsiorsky & Latash, 2008). 하위 계층(lower hierarchy)은 네 손가락(index, middle, ring, little fingers)으로 구성되며 virtual finger에 요구되는 기계적 효과가 각 손가락으로 분배된다. 따라서 안정적인 prehension을 위해서는 각 제어 계층에서 적절한 시너지 작용이 이루어져야 한다. 손가락 수직력(normal force)의 결합에 의해 형성되는 쥐는 힘(grip force)을 안정화 하는 시너지 작용은 전형적으로 계층 간 trade-off가 나타나는 것으로 알려져 있다. 상위 계층에서 서로 마주하는 thumb과 virtual finger의 normal force는 물체의 위치를 안정화하기 위해 서로 정적인 공변성(positive covariation)을 지니며 강력한 시너지 작용을 보이는 반면, virtual finger normal force를 안정화 하는 하위 제어 계층(네 손가락 간)의 시너지 작용은 존재하지 않는다는 것이다(Park et al., 2010). 외부 제약 조건에 따른 계층 간 시너지 작용을 확인하기 위해 자유 물체(free object)와 고정된 물체(fixed object)로 구분하여 접근한 이전 연구에서도 고정된 물체를 쥘 때 조차도 계층 간 trade-off 시너지가 유효하게 나타남을 확인하였다(Song et al., 2022).

Figure 1. A scheme of hierarchical control for multi-digit moment production including two control hierarchies. The Mi represents moment of i digit, and the MTOT stands for total moment. TH: thumb; VF: virtual finger; I: index; M: middle; R: ring; L: little finger

Modify Delete

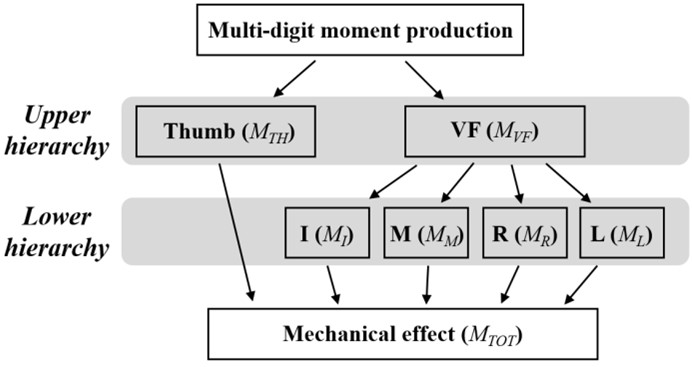
한편, 정적인 prehension에서 net moment를 안정화 하기 위한 손가락 moment의 공변성은 grip force를 안정화하는 패턴과 차이를 지닌다. 일정한 moment를 생산하기 위해서는 상위 계층의 thumb와 virtual finger가 서로 에러를 상쇄하는 부적 공변화(negative covariation) 패턴을 보여야 하며, 하위 계층 또한 네 손가락 moment가 virtual finger moment를 안정화 하기 위해 부적 공변성을 지녀야 한다. 이러한 moment 안정화를 위한 두 제어 계층 간 공변화 패턴의 일치는 grip force 시너지 패턴과는 다르게 계층 간 trade-off가 나타나지 않고, 두 계층 모두에서 시너지 작용이 존재할 수 있음을 의미한다. 따라서 본 연구의 첫 번째 목적은 moment 생산에 대한 계층적 시너지 작용의 특성을 확인하는 것이었으며 이를 위해 다섯 손가락을 이용해 물체를 쥐고 반복적으로 요구되는 moment를 생산하고 일정하게 유지하는 과제를 차용하였다. 그리고 이 과정에서 나타나는 grip force와 moment를 안정화 하는 계층적 시너지 작용을 정량화하고 비교하였다. 또한, 손가락을 이용한 물체에 moment 생성은 두 방향, 즉 회내(pronation)와 회외(supination) 방향으로 구분될 수 있기 때문에, 본 연구에서는 moment 생성 방향을 구분함으로써 moment 방향에 따른 손가락 moment 생성 전략과 계층적 시너지 작용을 확인하고자 하였다. 첫 번째 연구 가설은 다중 손가락의 force와 moment 생성 패턴과 연관되며 다음과 같이 설정되었다. Hypothesis 1: Grip force를 형성하는 상위 제어 계층의 thumb와 virtual finger의 normal force는 moment 생성 방향에 따라 다르지 않을 것이며, 반면 thumb와 virtual finger의 moment는 net moment의 방향에 따른 차이를 보일 것이다. 두 번째 가설은 계층적 시너지 구조와 연관되며 다음과 같이 설정되었다. Hypothesis 2: Moment를 안정화 하는 시너지 작용은 force에 대한 시너지 보다 모든 제어 계층에서 더 크게 나타날 것이며, 두 계층에 걸쳐 유의미한 시너지 작용이 나타날 것이다.

본 연구의 두 번째 목적은 하위 제어 계층인 네 손가락의 제어적/기능적 분화(finger specialization)를 확인하는 것이었다. 다섯 손가락으로 force와 moment를 생성하여 물체를 정적으로 잡는 경우, moment가 작용하는 회전축(물체의 질량 중심)에서 멀리 떨어진 손가락인 검지(index)과 소지(little finger)는 가쪽 손가락(lateral finger)으로 정의되며, moment의 생성과 제어에 크게 기여하는 것으로 알려져 있다(Park, Baum, Kim, Kim & Shim, 2012; Shim, Latash & Zatsiorsky, 2004; Zatsiorsky, Gao & Latash, 2003). 반면, 네 손가락 중 moment 생성 기여가 상대적으로 작은 중지(middle)와 약지(ring finger)는 안쪽 손가락(medial finger)으로 구분되며, thumb의 normal force에 대응하여 grip force를 생성하는데 주된 작용을 하는 것으로 보고된다(Zatsiorsky & Latash, 2008). 본 연구에서는 이러한 손가락의 제어적/기능적 분화가 moment와 force를 안정화 하는데 기여하는 정도를 정량화 하여 비교하기 위해 다음과 같은 가설을 수립하였다. Hypothesis 3: Moment를 안정화 하는 손가락 간의 시너지 작용은 lateral finger가 medial finger 보다 클 것이다. 또한, virtual finger와 thumb의 grip force 안정화 작용을 반영하여 손가락 간 정적 공변성은 medial finger가 lateral finger 보다 더 크게 나타날 것이다.

1. 대상자

실험 수행에 영향을 미칠 수 있는 상지의 근골격계 및 신경계 손상이 없는 성인 남성 12명(연령: 29.4±4.3세; 체중: 77±6.43 kg; 신장: 1.76±0.09 m)이 연구에 참여하였다. 우세 손(hand dominance)을 확인하는 에딘버러 검사(Edinburgh handedness test)를 통해 모든 참가자들이 오른손잡이 임을 확인하였다. 모든 연구 절차는 서울 소재 S대학교 기관생명윤리위원회의 권고에 따라 수행되었다. 참가자들의 자발적 연구 참가를 확인하기 위해 승인된 동의서를 사전에 작성한 후 실험이 진행되었다.

2. 실험도구

다섯 손가락(thumb, index, middle, ring, little) 끝으로 핸들을 잡고 등척성 조건에서 moment를 생성할 수 있는 실험용 핸들이 고안되었다(Figure 2B). x-z 평면에 정렬된 핸들에는 개별 손가락 힘을 측정하기 위해 6축 힘 센서(Nano-17, ATI Industrial Automation, Garner, NC, USA) 5개가 부착되었다. 네 손가락에 해당하는 힘 센서는 x 축을 따라 30 mm 간격으로 배치되었다. 그립 폭(grip width) — thumb에 해당하는 센서 표면과 네 손가락 센서 표면의 z 축 거리 — 는 50 mm로 설정되었다. 손가락과 접촉되는 각 힘 센서의 표면에는 손가락과 마찰을 증가시키기 위해 100-grit의 사포가 부착되었다. 손가락 끝과 사포 간 마찰 계수는 약 1.4~1.5였다(Savescu, Latash & Zatsiorsky, 2008). 핸들은 스틸 프레임에 의해 지면에서 150 mm 높이게 견고하게 고정되었으며, 실험용 책상 위에 놓여졌다.

Figure 2. Experimental setup. (A) The rigid forearm brace on the table held the participant's right forearm and wrist securely in a neutral prehension position. A monitor located at eye level approximately 0.7 m away from the participant was used for visual feedback on digit total moment (MTOT). (B) Description of the experimental handle. Five 6-component force transducers were aligned in the x-z plane to measure the individual digit forces. The axis of the moment along the y-axis was located at the mid-point of the grip width.

Modify Delete

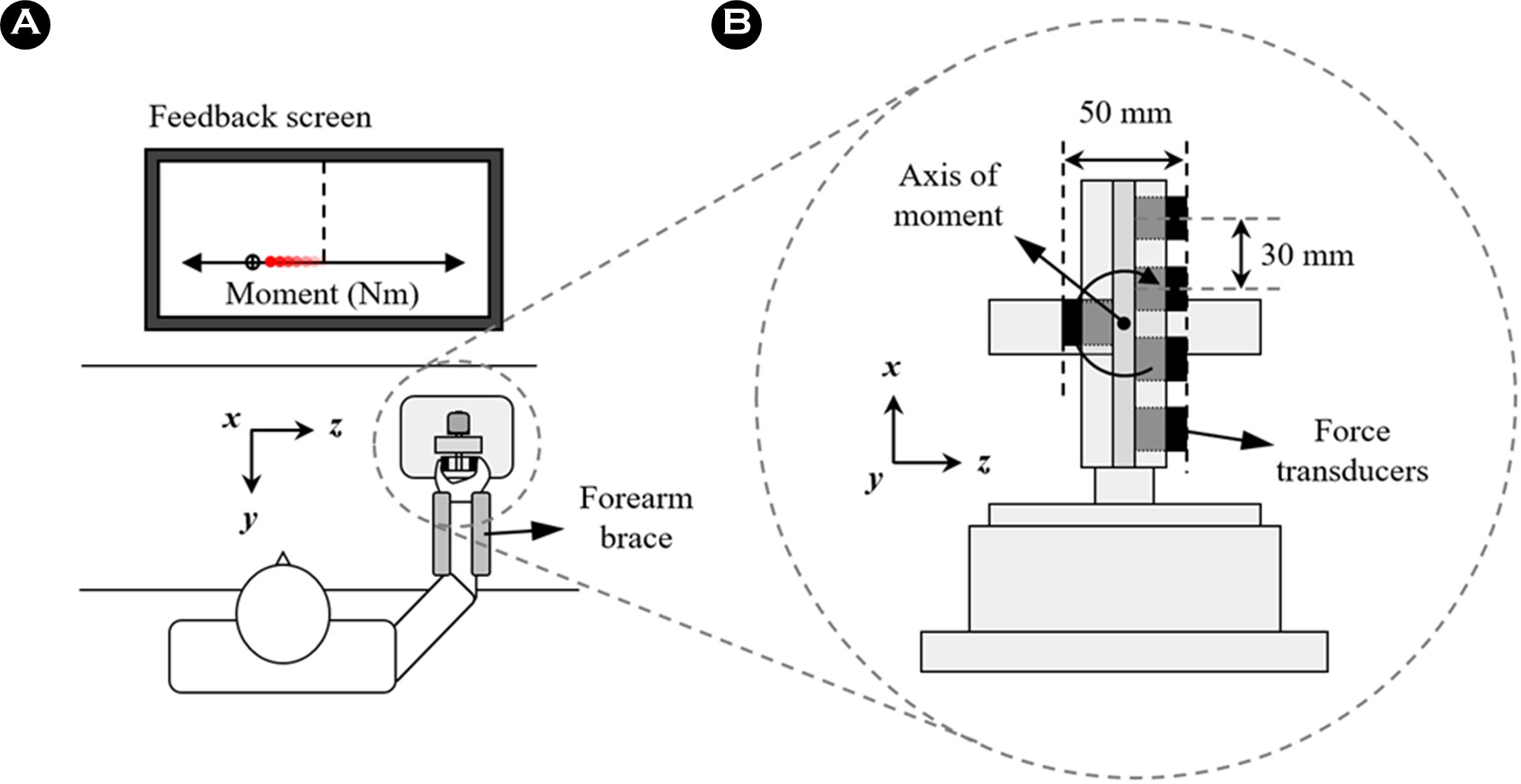
힘 센서를 통해 수집된 모든 신호는 200 Hz로 샘플링되어 아날로그-디지털 변환기(Gen5, AMTI, Watertown, MA, USA)를 통해 디지털화 되었다. 24인치 모니터가 실험용 책상 위에 놓여져 실시간으로 손가락 moment에 대한 정보를 참가자에게 제공하였다. 손가락 힘의 수집과 moment 산출, 시각 피드백 제공을 위해 맞춤형 LabVIEW program (National Instruments)이 사용되었다.

3. 실험절차

참가자들은 실험용 책상 앞에 앉아 오른 팔 전완과 손목을 받침대에 고정하였으며, 각 손가락 끝을 각 힘 센서 중앙에 위치하도록 핸들을 잡으라고 지시 받았다(Figure 2A). 실험 과제는 등척성 조건에서 다섯 손가락을 이용해 요구되는 목표 모멘트(target moment)를 핸들에 생성하고 유지하는 것이었다. Target moment는 두 방향에 대해, 회내(pronation) 방향으로 0.4 Nm, 회외(supination) 방향으로 -0.4 Nm로 설정되었다. 따라서 각 참가자는 두 가지 moment 조건에 대한 실험을 수행했다.

텍스트 상자각 시도(trial)는 15초 동안 이뤄졌다. 참가자는 측정이 시작된 후 3초 이내에 다섯 손가락의 moment 합(total moment, )에 대한 실시간 피드백을 받으며 target moment에 가능한 정확하게 일치시키고 일정하게 유지하도록 지시 받았다. 모니터의 템플릿에는 target moment의 위치와 함께 의 크기가 수평축을 따라 움직이는 커서(cursor)로 나타났다. 회내 방향에서 커서는 왼쪽으로, 회외 방향에서 커서는 오른쪽으로 moment의 크기에 따라 이동했다. 피드백으로 제공된 는 y 축을 따르는 고정된 회전축에 대해 Equation 1을 통해 실시간으로 계산되었다.

각 moment 조건은 20회 반복 측정되어 총 40회의 시도(2 moment 조건 × 20회 시도)가 수행되었다. 실험은 이틀에 걸쳐 진행되었다. 첫째 날에는 참가자들이 실험 설정과 과제에 익숙해지도록 연습 세션을 가졌으며, 둘째 날에는 두 moment 방향에 대한 실험 과제를 무작위 순서로 진행하였다. 매 시도 마다 참가자들에게 의무적으로 40초의 휴식 시간이 부여되었으며, 피로를 보고할 경우 추가적인 휴식 시간을 제공했다.

4. 자료분석

수집된 개별 손가락의 힘 데이터는 10 Hz의 컷오프 주파수를 지닌 4차 저역통과 필터(zero-lag 4th order low-pass Butterworth filter)로 필터링 되었다. y 축을 따르는 고정된 회전축에 대한 개별 손가락의 moment ()와 는 z 축 힘인 normal force ()와 x 축 힘인 tangential force ()를 이용해 산출되었다.

아래 첨자 i는 개별 손가락을 나타내며, d와 r은 각각 normal force와 tangential force의 moment arm에 해당한다. Virtual finger를 포함하여 핸들의 고정된 축에 대한 개별 손가락의 moment가 산출되었다. 산출된 모든 손가락의 moment와 normal force는 이후 비제어다양체(uncontrolled manifold, UCM) 분석에 활용되었다.

UCM 분석은 과잉된 요소 변인(redundant elemental vari- ables, EV)의 차원에서 반복적인 과제 수행 동안 나타난 분산을 통해 수행 변인(performance variable, PV)을 안정화 하는 정도를 synergy 지수로 정량화 하는 방법으로서 동적 안정성 지표(dynamic stability)로 활용되어 왔다(Scholz & Schoner, 1999; Song, Shin et al., 2021). 특히, 본 연구에서는 두 제어 계층 간 차이를 확인하기 위해 상위 제어 계층(upper hierarchy)과 하위 제어 계층(lower hierarchy) 각각에 대해 UCM 분석을 개별적으로 적용하였다. 또한, moment와 grip force를 안정화 하는 시너지 지수를 산출하기 위해 손가락 moment와 normal force의 두 차원에서 UCM 분석을 수행하였다.

EV 차원의 분산은 두 부분 공간, UCM 공간과 그에 직교하는 orthogonal (ORT) 공간으로 분해된다. UCM 공간은 PV를 변화시키지 않는, 즉 안정화 하는 부분 공간인 반면, ORT 공간은 PV의 변화를 야기하는 공간이 된다. 상위 계층에서 PV는 모든 손가락 moment와 normal force의 합인 와 로 설정되었으며, EV는 thumb과 virtual finger의 moment와 normal force (i.e., [, ] & [, ])로 설정되었다. 하위 계층의 경우, 네 손가락의 기계적 효과를 반영하는 와 가 PV로 설정되었으며, 개별 손가락의 moment []와 normal force []가 각각 EV로 설정되었다. PV의 변화는 다음과 같이 EV에 대함 함수로 표현된다.

J는 반복적인 과제 시도에서 나타나는 EV의 미소 변화와 PV의 변화를 연결하는 자코비안 행렬을 의미한다. 상위 계층에 대한 자코비안 행렬은 net moment를 PV로 하는 분석에 대해 [1, 1]로, grip force를 PV로 하는 분석에 대해 [1, -1]로 설정되었으며, 하위 계층의 분석은 모두 [1, 1, 1, 1]로 설정되었다. UCM 공간은 자코비안 행렬의 영공간(null space)에 의해 정의되며, 이를 통해 UCM 공간의 분산()과 이에 직교하는 ORT 공간의 분산()을 산출하였다. 시너지 지수(ΔV)는 VUCM과 VORT의 차이로 다음과 같이 산출되며, 총 분산()로 정규화 된다.

각 분산은 각 부분 공간이 지닌 자유도(degrees of freedom, DOF)에 의해 추가로 정규화 되어 서로 다른 차원에서 관찰된 두 부분 공간 간의 비교를 가능하게 한다. 이후, 산출된 ΔV는 통계 분석을 위해 Fischer transformation을 이용해 로그 변환되었다. 추가적으로, lateral finger와 medial finger에 대해 moment와 normal force를 안정화 하는 ΔV가 동일한 UCM 분석 과정을 통해 산출되었다.

5. 자료처리

모든 종속 변인의 통계 분석에 SPSS 24.0 (IBM, Armonk, NY, USA)이 사용되었다. Moment 생성 방향에 따른 thumb과 virtual finger가 지니는 기계적 효과의 차이를 확인하기 위해 Finger (thumb / virtual finger)와 Direction (pronation / supination)을 요인으로 하는 Repeated-measures (RM) ANOVA를 moment와 normal force에 대해 각각 수행하였다(Hypo- thesis 1). 과제 수행 동안 moment와 grip force를 안정화 하는 정도를 비교하기 위해 각 제어 계층에서 획득된 synergy 지수(ΔV)에 대해 손가락의 기계적 효과를 구분한 Effect (moment / normal force)와 Direction을 요인으로 하는 RM ANOVA를 각 제어 계층을 구분하여 수행하였다(Hypothesis 2). 또한, lateral과 medial finger 간 moment와 normal force를 안정화 하는 ΔV의 차이를 확인하기 위해 Finger (lateral / medial finger)를 요인으로 하는 RM ANOVA를 적용하였다(Hypo- thesis 3). 추가적으로, synergy 작용의 강도를 평가하기 single-sample t-test를 통해 모든 ΔV가 임계값(critical value)과 비교되었다. 상위 계층과 하위 계층에서 임계값은 각각 0과 0.55로 설정되었으며, 이를 초과하면 유의미한 synergy 작용이 있었음을 의미한다. Mauchly's sphericity test가 구형성 가정을 확인하는데 사용되었으며, Greenhouse-Geisser estimation을 통해 구형성 위반에 대한 보정이 이루어 졌다. 유의한 요인 간 상호작용 효과에 대해 Bonferroni corrections을 동반한 사후 분석이 수행되었다. 모든 검정 유의 수준(α)은 0.05 미만으로 설정하였다.

1. 상위 제어 계층의 손가락 모멘트 및 힘 생성 효과

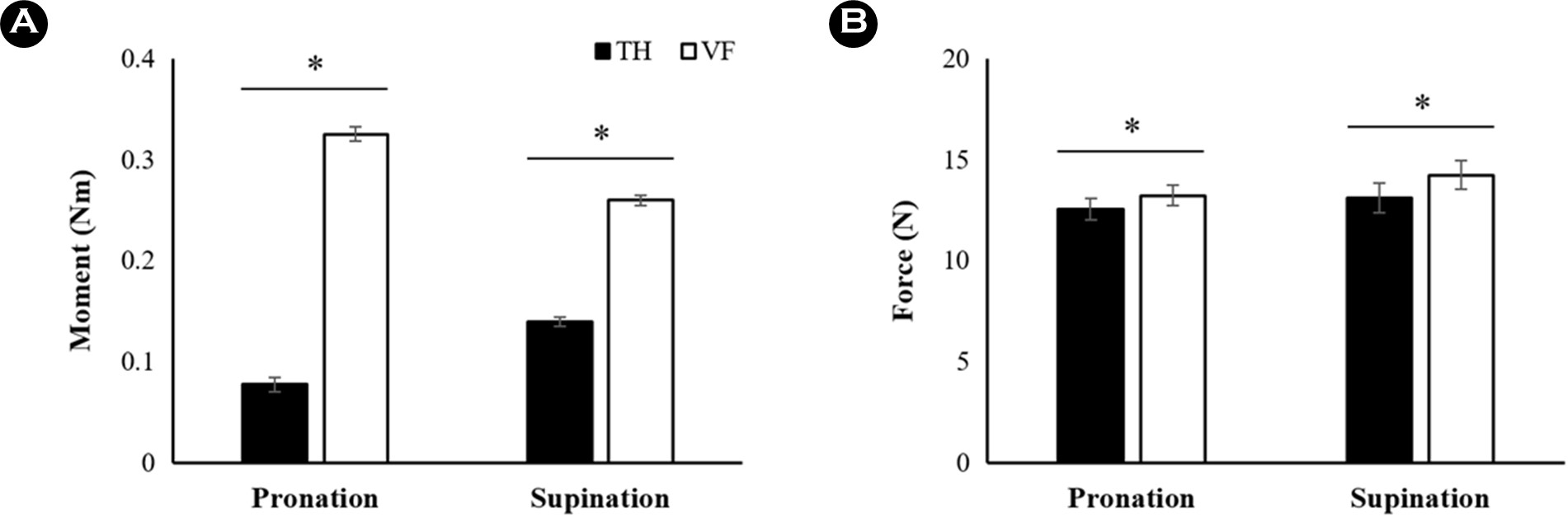
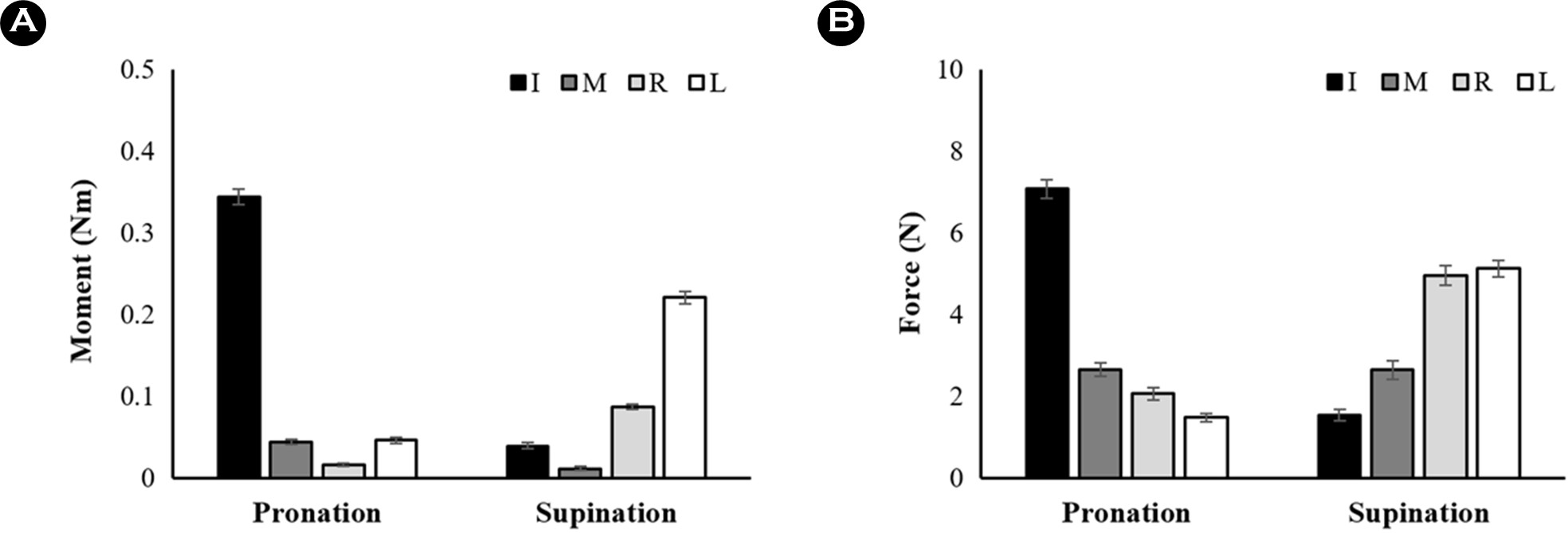
Thumb과 virtual finger의 moment에 대한 Finger × Direc- tion RM ANOVA 결과, Finger (F[1,11] = 355.95, p < 0.001, ηp2 = 0.97)와 Direction (F[1,11] = 14.19, p = 0.003, ηp2 = 0.56)에 대한 주효과와 요인 간 상호작용(F[1,11] = 83.6, p < 0.001, ηp2 = 0.88) 효과가 확인되었다. 사후 분석 결과, virtual finger의 moment는 항상 thumb의 moment 보다 컸으며, thumb의 moment는 supination 방향에서 pronation 방향에 비해 상대적으로 더 큰 반면, virtual finger의 moment는 pronation 방향이 더 컸음이 확인되었다(Figure 3A).

Grip force를 생성하는 thumb과 virtual finger의 normal force는 Finger (F[1,11] = 19.12, p = 0.001, ηp2 = 0.64)에 대한 주효과 만이 나타났다. 이는 virtual finger의 normal force가 thumb 보다 유의하게 컸으며, moment 생성 방향에 따른 차이는 존재하지 않음을 의미한다(Figure 3B).

Figure 3. Magnitudes of (A) digit moments and (B) normal forces under pronation and supination moment production. The data shown as means and standard errors. The solid bars indicate thumb, while the open bars represent virtual finger. The asterisks (*) indicate significant differences between digits.

Modify Delete

2. 손가락 모멘트와 힘을 안정화 하는 계층적 시너지 작용

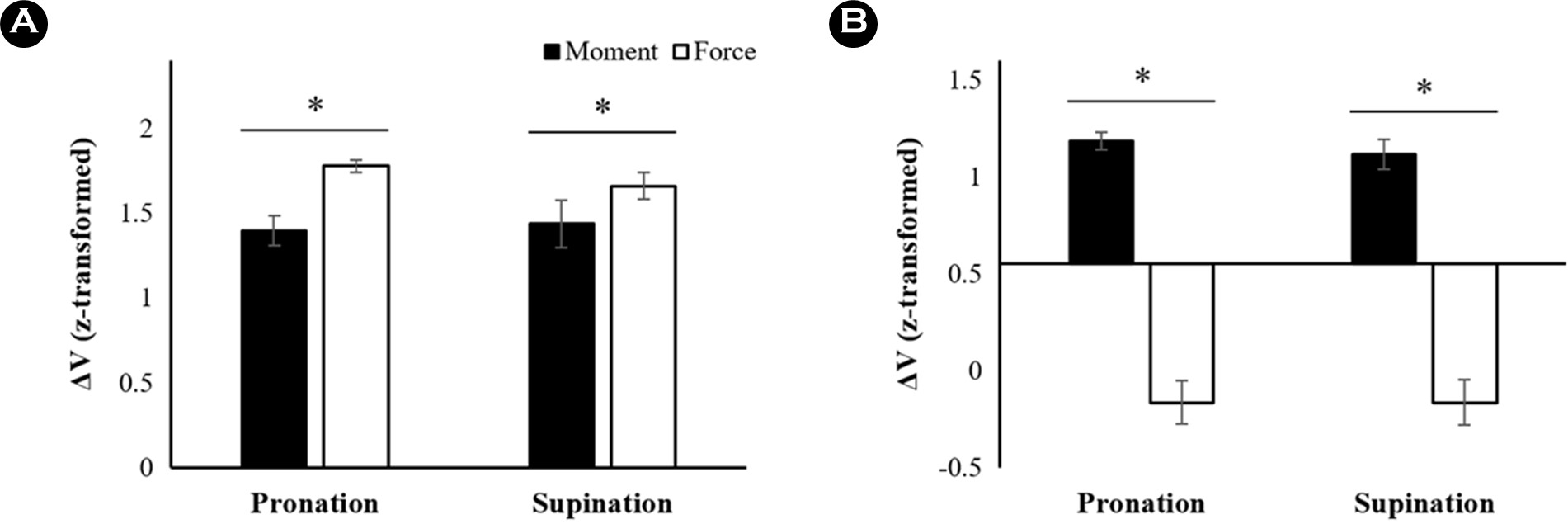
Figure 4A는 net moment와 grip force를 안정화 하는 상위 제어 계층의 synergy 작용을 보여준다. Grip force를 안정화 하는 synergy 지수(ΔV)는 moment 안정화 ΔV 보다 크게 나타났다. 두 ΔV는 moment 생성 방향에 따라 차이를 보이지 않았다. 이러한 결과는 통계적으로 유의한 Effect의 주효과(F[1,11] = 7.58, p = 0.019, ηp2 = 0.41)에 의해 확인되었다. Single-sample t-test를 이용해 임계 ΔV(0)와 모든 조건에서 획득된 ΔV를 비교한 결과, 상위 계층의 moment와 grip force를 안정화 하는 ΔV는 모든 조건에서 임계값을 상회 하는 것으로 나타났다(all p<0.001).

Virtual finger의 moment와 normal force를 안정화하는 하위 제어 계층의 ΔV에 대한 결과는 Figure 4B에 나타난다. RM ANOVA 결과, 상위 계층과 유사하게 Effect (F[1,11] = 200.37, p < 0.001, ηp2 = 0.95)에 대한 주효과 만이 확인되었다. 이는 moment를 안정화 하는 synergy 작용이 normal force를 안정화 하는 synergy 보다 더 크게 나타났으며, moment 방향에 따른 차이는 없음을 의미한다. Single-sample t-test 결과, moment를 안정화 하는 ΔV만이 임계값(0.55)을 유의하게 초과하여 유의미한 synergy 작용이 있음이 확인되었다(all p<0.001).

Figure 4. Magnitudes of synergy index (ΔV) for (A) upper and (B) lower hierarchy under pronation and supination moment production. The data shown as means and standard errors. The solid bars indicate ΔV for stabilization of digit moment, while the open bars represent normal force stabilizing ΔV. The asterisks (*) indicate significant differences between two sets of ΔV.

Modify Delete

3. 손가락 모멘트와 힘 생산을 위한 손가락 기능적 분화 작용

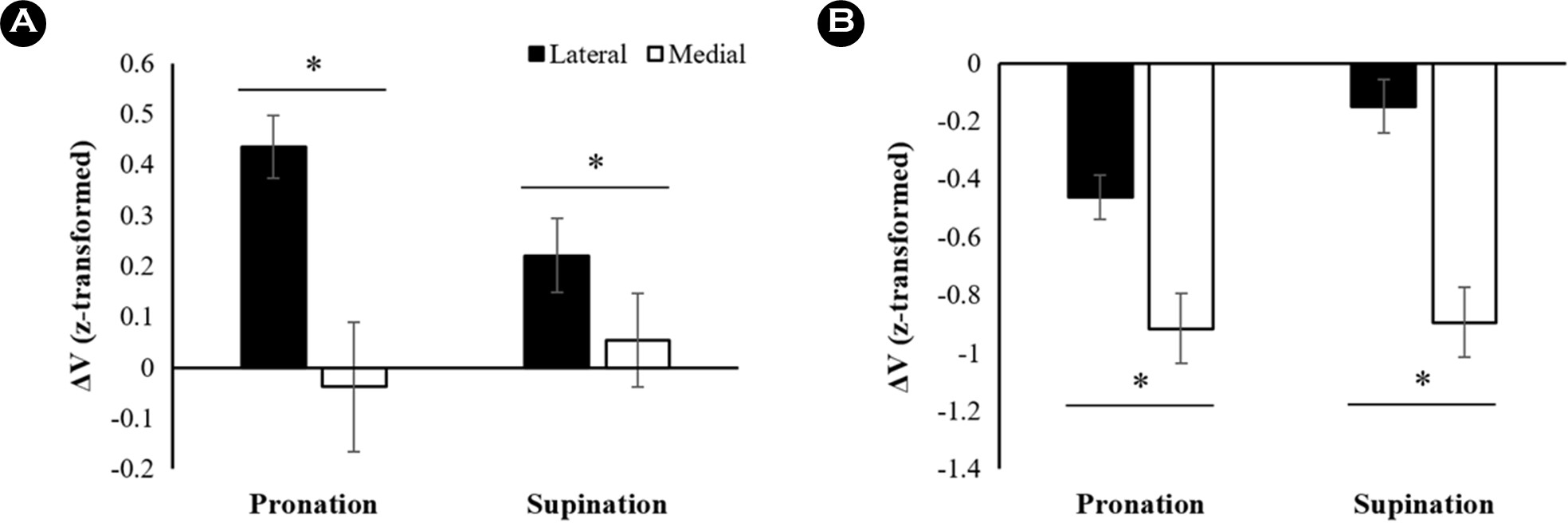
Moment를 안정화 하는 lateral finger와 medial finger의 작용을 비교한 결과, lateral finger의 ΔV는 medial finger 보다 유의하게 컸으며, moment 방향에 따라 차이가 나지 않았다(Figure 5A). 이는 Finger를 요인으로 하는 유의한 주효과(F[1,11] = 13.21, p = 0.004, ηp2 = 0.55)에 의해 확인되었다. Single-sample t-test 결과, lateral finger에서만 moment를 안정화 하는 유의미한 synergy 작용이 있음이 확인되었다(all p<0.001).

Normal force에 대한 medial finger의 ΔV는 lateral finger의 ΔV 보다 유의하게 작았으며, moment 생성 방향에 따른 차이를 보이지 않았다(Figure 5B). 이 결과는 Finger를 요인으로 하는 유의한 주효과(F[1,11] = 45.46, p < 0.001, ηp2 = 0.81)에 의해 확인되었다. Lateral과 medial finger의 ΔV 모두 유의미한 synergy 효과를 반영하는 임계값에 이르지 못함이 single-sample t-test를 통해 확인되었다.

Figure 5. Average magnitudes of synergy index (ΔV) for stabilization of (A) moments and (B) normal forces under pronation and supination moment production. The solid bars correspond to lateral finger, and the open bars indicate medial finger. The asterisks (*) indicate significant differences of ΔV between lateral and medial fingers.

Modify Delete

본 연구는 운동요소의 과잉이 내재된 인간의 기능적 움직임인 다중 손가락을 이용한 쥐기, 즉 multi-digit prehension을 통해 과잉된 운동요소의 계층적 조직화(hierarchical organ- ization of redundant elements) 특성을 살펴보고자 하였다. 특히 다중 손가락의 moment 생성에 초점을 맞추어 고정된 핸들에 요구되는 moment를 생산하는 동안 moment와 force를 안정화 하는 전략을 구분하여 확인하였다. Thumb와 virtual finger가 생산하는 normal force의 크기는 moment 생성 방향에 따라 다르지 않았던 반면, moment는 방향에 따른 유의한 차이를 보여주었다(Figure 3A). 이는 본 연구의 첫 번째 가설과 일치한다. Pronation과 supination 방향에서 요구되는 net moment는 0.4 Nm로 동일했으며, 따라서 이 결과는 상위 계층의 두 손가락 moment는 방향에 따라 net moment 생성에 다르게 기여함을 의미한다. Thumb의 moment는 pronation 방향 보다 supination에서 더 컸으며, virtual finger의 moment는 반대 패턴을 보였다. Thumb은 위치적 특성으로 인해 다른 손가락 보다 작은 moment arm을 갖으며, 따라서 thumb에 의한 moment 생산 기여가 증가되는 것은 비 효율적인 전략으로 여겨질 수 있다. 이러한 방향에 따른 moment 크기의 차이는 하위 계층인 네 손가락의 moment 방향에 따른 moment 생성 능력의 차이에서 기인한 것으로 보인다. Figure 6A와 6B는 개별 손가락이 생성한 moment와 force의 크기를 보여준다. Pronation moment를 만드는 주된 손가락(agonist finger)인 index finger 보다 supination 방향의 주된 손가락인 little finger가 상대적으로 작은 moment를 발휘하는 것을 확인할 수 있다. 즉, supination 방향에 대한 하위 계층의 상대적으로 작은 moment 생성 능력을 상위 계층인 thumb이 긍정적으로 보상하여 요구되는 net moment를 만족시킨 결과인 것이다.

Figure 6. Average magnitudes of individual fingers' (A) moments and (B) normal forces under pronation and supination moment production. The black bars, dark grey bars, light grey bars, and open bars represent index (I), middle (M), ring (R), and little (L) fingers, respectively.

Modify Delete

Moment 방향에 따른 손가락의 moment 생성 능력의 차이에도 불구하고 moment와 force를 안정화 하는 계층적 시너지 모두 방향에 따른 차이를 보이지 않았다. 상위 제어 계층에서는 moment와 grip force 모두를 안정화 하는 강한 시너지 작용이 나타났으며, grip force의 시너지 작용은 moment에 대한 시너지 작용보다 상대적으로 더 컸다. 이점은 수행된 실험 과제가 목표 moment를 생성하고 유지하는 것이었기 때문에, moment를 안정화 하는 작용이 더 클 것이라 기대했던 본 연구의 가설과 반대되는 결과였다. 상위 계층에서 moment와 force에 대한 시너지 작용은 thumb와 virtual finger에 서로 다른 공변화 패턴을 요구한다(Park, Han & Shim, 2015). Thumb와 virtual finger의 moment는 net moment를 안정화 하기 위해 정적인 공변성을 지녀야 하며, 반대로 thumb와 virtual finger의 normal force는 서로 정적 공변성을 지녀야 한다. 이렇듯 두 손가락 간 서로 다른 공변화 패턴이 동시에 발생했다는 것은 moment의 크기를 조정하는데 있어서 손가락 normal force의 크기 보다는 tangential force와 moment arm과 같은 다른 요인을 변화시킴으로써 moment를 생성 및 제어했음을 의미한다. 이러한 전략은 로봇의 복잡한 prehension 제어를 단순화 하기 위해 제안된 중첩의 원리(principle of superposition)로 해석될 수 있다(Arimoto & Nguyen, 2001). 중첩의 원리는 물체의 translation과 rotation 제어가 동시에 요구되는 상황에서 컨트롤러는 force와 moment 생성에 대한 독립적인 하위 운동명령(motor command)을 통해 제어할 수 있다는 것이며, 인간의 prehension에서도 나타나는 특성임이 여러 실험을 통해 확인되었다(Shim & Park, 2007; Song, Kim et al., 2021; Zatsiorsky, Latash, Gao & Shim, 2004). 본 연구 결과는 이 중첩의 원리가 고정된 물체에 대해 moment를 생성하는 과제 상황에서도 유효하게 나타날 수 있음에 대한 근거 자료가 된다.

또한, moment에 대한 요구사항과 피드백 만이 존재했고, 핸들이 외부에 고정된(fixed object) 조건임에도 불구하고 더 강하게 나타난 grip force 안정화 시너지 작용은 thumb와 virtual finger normal force의 공변화 패턴에 대한 중요한 시사점을 갖는다. 외부 장치에 고정되지 않은 자유 물체와 고정된 물체를 잡는 두 가지 prehension 과제는 외부에 의한 기계적 제약(mechanical constraints)의 차이를 지닌다. 자유 물체를 손으로 잡고 정적인 prehension을 수행한다면, 상위 제어 계층의 마주하는 thumb와 virtual finger의 normal force는 서로의 힘을 상쇄하여 완벽한 정적 공변화(positive covariation) 패턴을 보일 것이다(Song et al., 2022). 그러나 본 연구와 같이 고정된 핸들을 쥘 때는 손가락의 normal force가 제약되지 않으며, 이때 특정한 방식으로 나타나는 요소 간 공변화 패턴은 신경계에 내재된 제어 전략을 반영하는 것으로 해석된다(Park et al., 2012; Shim et al., 2004; Song et al., 2022). 따라서 본 연구에서 관찰된 grip force에 대한 강한 시너지 작용은, prehension 동안 thumb와 virtual finger normal force 간 정적인 공변성이 발생하는 것이 기계적 제약 조건이나 요구되는 과제의 지시사항에서 기인한 것이 아닌, CNS에 내재된 고유한 제어 전략일 수 있음을 시사한다.

하위 제어 계층에서는 전형적인 계층 간 trade-off 시너지를 반영하여 virtual finger normal force를 안정화 하는 시너지 작용은 임계 수준에 미치지 않았으며, 손가락 간 normal force는 정적인 공변화 패턴을 보였다(Figure 4B). 반면, 상위 계층과 유사하게 하위 계층에서도 moment를 안정화 하는 유의미한 시너지 작용이 확인되어 네 손가락의 moment는 서로의 오류를 상쇄하는 부적 공변성을 띄었음을 확인하였다(Figure 4A). 이 결과와 유사하게, 손가락 중 moment 생산을 담당하는 lateral finger의 moment에 대한 시너지 작용은 medial finger보다 크게 나타났고, normal force의 정적 공변성은 오히려 medial finger에서 더 크게 나타났다(Figure 5). 이는 본 연구의 두 번째와 세 번째 가설과 일치한 결과였다. Trade-off 시너지, 즉 Prehension 동안 상위 계층에서만 관찰되는 유의미한 시너지 작용은 CNS가 제어 계층 중 과제 수행과 연관된 상위 레벨에 주로 관심을 두며 하위 제어 계층에 운동요소의 조직화는 이차적으로 고려하는 것으로 여겨져 왔다(Latash, Gorniak & Zatsiorsky, 2008). 그러나 본 연구에서 확인된 하위 계층에서도 두드러진 moment 안정화 시너지는 신경계가 과제 특성을 반영하여 여러 계층 수준에서 동시에 시너지를 형성할 수 있음을 시사한다. 선행연구에서는 회전 평형(rotational equilibrium)의 안정화는 과제 수준에서 요구되지 않더라도 나타나는 기본적 제어 전략이라 보고하였으며, 손에 쥔 물체의 평형을 해치는 외력이 작용할 경우에 신경계는 물체를 쥐는 힘 보다 회전 제어에 더 중점을 둔다고 보고하였다(Scholz et al., 2002). 이러한 회전 평형에 대한 우세한 제어적 특성은 하위계층에서 두드러진 moment 안정화 작용의 원인이 될 수 있다. 또한, 회전축이 네 손가락의 중앙(i.e., medial과 ring finger의 사이)에 위치하는 경우 네 손가락 normal force의 정적인 공변성은 moment를 안정화하는 부가적인 효과(minimization of the secondary moment prin- ciple)를 발휘하게 되며(Li, Latash, Newell & Zatsiorsky, 1998; Zatsiorsky & Latash, 2008), 이러한 네 손가락이 생산하는 기계적 효과의 특성 또한 본 결과에 영향을 미쳤을 것으로 사료된다.

본 연구는 다중 손가락을 이용한 두 방향의 moment 생성 과제를 통해 prehension 동안 나타나는 계층적 제어 특성과 과잉된 운동요소를 조직화 하는 전략을 확인하고자 하였다. 동일한 net moment를 생산하는 동안 상위 제어 계층의 thumb와 virtual finger의 moment 크기는 moment 방향에 따라 차이를 보였으며, 이는 하위 계층인 네 손가락이 지닌 moment 생성 능력의 차이에서 기인하는 것을 확인하였다. 비제어다양체(UCM) 분석을 통해 정량화한 계층적 시너지 작용은 물체에 작용하는 grip force와 moment 차원에서 다르게 나타났다. Force를 안정화 하는 시너지 작용은 전형적인 계층 간 trade-off 시너지 형태로 나타난 반면, moment 안정화 시너지는 두 제어 계층 모두에서 유의하게 나타났다. 이 결과는 신경계에 내제된 고유한 grip force 생성 특성과 함께 과잉된 운동요소의 시너지 작용은 과제 수행의 안정성을 위해 두 제어 계층에서 동시에 조직화 될 수 있음을 시사한다. 또한, 추가적으로 손가락의 기능적 분화(finger specialization)와 연관된 가설을 검정하였으며, 본 연구에서 도출된 결과는 lateral finger와 medial finger가 지닌 기능적 차이에 대한 선행연구의 제안을 지지한다.