Development and research on running shoes are continuously carried out in that the difference in running shoes' properties affects the impact delivered to the human body and the load to the lower extremity joint (Agresta, Kessler, Southern, Goulet, Zernicke & Zendler, 2018; Baltich, Maurer & Nigg, 2015; Ha, Ryu & Gil, 2020; Kulmala, Kosonen, Nurminen & Avela, 2018; Lam, Liu, Wu, Liu & Sun, 2019; Lam, Ng & Kong, 2017; Lewinson, Worobets & Stefanyshyn, 2016; Meardon, Willson, Kernozek, Duerst & Derrick, 2018; Nigg, Bahlsen, Luethi & Stokes, 1987).

Even though the peak of vertical ground reaction force (PVGRF) was higher as the shoes were thicker, based on recent research that examined 12 types of shoes' mechanical characteristics and the correlation with impact absorption function (Ha et al., 2020), it was reported that the vertical loading rate (VLR) was smaller as the revelation time of PVGRF increased. In research that investigated the effects of shoe's cushioning on the impact of running (Meardon et al., 2018), it was reported that VLR was smaller in goods cushioning and soft (low hardness) shoes than hard (high hardness) shoes. Based on the above researches, it is judged that the thickness and properties of shoes critically affect impact absorption.

Nonetheless, there is insufficient research examining the effects of shoes' thickness and properties on the stability and consistency of the lower extremity joint motions during running. Practical methods examining the stability and consistency of repetitive human body motions such as running are to look at variability with nonlinear time-series methods (Buzzi, Stergiou, Kurz, Hageman & Heidel, 2003; Dingwell & Cusumano, 2000; Dingwell, Cusumano, Sternad & Cavanagh, 2000; Hausdorff, Forman, Ladin, Goldberger, Rigney & Wei, 1994; Ryu, 2006, 2007, 2008, 2009, 2014). Of the nonlinear methods, Lyapunov exponent (LyE) has been used in researches examining the dynamic stability and consistency of repetitive walking and running (Ryu, 2006, 2007, 2008, 2009, 2014), and it has an advantage that the sensitivity to local shaking of the lower extremity joint can be directly evaluated (Kantz & Schreiber, 1997). In research that compared the dynamic stability of the lower extremity joint depending on walking speed (Ryu, 2007), it was reported that consistency and stability of the lower extremity joint motions were revealed, as LyE on knee joint was smaller in preferred speed walking compared to slow or quick walking. Namely, LyE has its value because LyE can predict comfort, including consistency and dynamic stability in human repetitive motions such as walking and running, and LyE is expected to play an important role in evaluating running shoes.

In the above research (Ha et al., 2020), part of the lower extremity joint motions depending on the properties of shoes was examined through the linear time-series methods. However, great distort and errors may occur due to data's temporal variation or change (Ryu, 2006, 2007, 2008, 2009, 2014). Moreover, it is difficult to explain and interpret the dynamic stability or consistency of the lower extremity joint in that a comparison was made with the values at a moment or the mean value.

Upon running between three types of running shoes with different properties, this research examined the differences of impact variables (PVRGF, VLR) and the dynamic stability variables (LyE) of the lower extremity joint angle (dorsiflexion/ plantarflexion angle at the ankle [DPA], inversion/eversion angle at ankle [IEA], flexion/extension angle at the knee [FEA]), and the lower extremity joint's angular velocity (dorsiflexion /plantarflexion angular velocity at ankle [DPAV], inversion/eversion angular velocity at ankle [IEAV], and flexion/extension angular velocity at the knee [FEAV]). Consequently, this research aimed to examine the effects of running shoes' properties on the impact variables and the lower extremity joint's dynamic stability and consistency. The hypo- theses of this research are as follows: First, as running shoes are thicker, VLR becomes smaller. Second, as the running shoes are thicker, the LyEs of DPA, IEA, FEA, DPAV, IEAV, and FEAV will be larger.

1. Participants

The participants in this research were 12 males in their 20s wearing 270 mm running shoes without orthopedic disease history (Age: 22.0±3.3 years, Height: 177.2±4.1 cm, Weight: 74.3±9.6 kg). Experiments were carried out for those who voluntarily agreed to the research ethics regulations.

2. Shoe characteristics

Figure 1. Control shoes (N: Nike react infinity, FA: Fila prototype A, FB: Fila prototype B)

Modify Delete

Figure 2. Impact tester (CompITS v5.0, Exeter Research, Inc., USA)

Modify Delete

The shoes used in this research were one type of running shoes of N company and two types of F company (FA, FB), as shown in (Figure 1). The properties of the running shoes were measured with an impact tester (CompITS v5.0, Exeter Research, Inc., USA; 3,000 Hz) by removing all uppers. Regarding the measuring method, the properties were measured by dropping a missile (Weight: 8.5 kg, diameter: 45 mm) from 50 mm above the rearfoot located at 12% in the direction from heel to toe as shown in (Figure 2) (Determan, Nevitt & Frederick, 2009; Ha et al., 2020).

3. Procedures

Figure 3. Experimental set-up

Modify Delete

The participants attached 19 reflective markers (Right leg - thigh: 4, shank: 4, knee joint: 2, ankle joint: 2, shoe: 7) to each segment and joint for modeling the lower extremity after enough preparatory exercise. As shown in (Figure 3), the running motions at 3.5 m/s on the treadmill (Instrumented treadmill, Bertec, USA) were sampled (shot) with 8 infrared cameras (Miqus 3, Qualisys, Sweden). All participants wore the three types of running shoes randomly, the sampling rate was set to 120 Hz, and 20 strides were collected.

4. Data processing

Figure 4. Impact variables of the PVGRF and the VLR (Ryu & Park, 2020)

Modify Delete

The 3D coordinate values of the reflective markers attached to the human body segments and joints during the running were obtained through the Qualisys Track Manager software (Qualisys, Sweden). The impact variables (PVGRF and VLR) and the lower extremity joint dynamic stability variables (LyEs of DPA, IEA, FEA, DPAV, IEAV, and FEAV) were calculated.

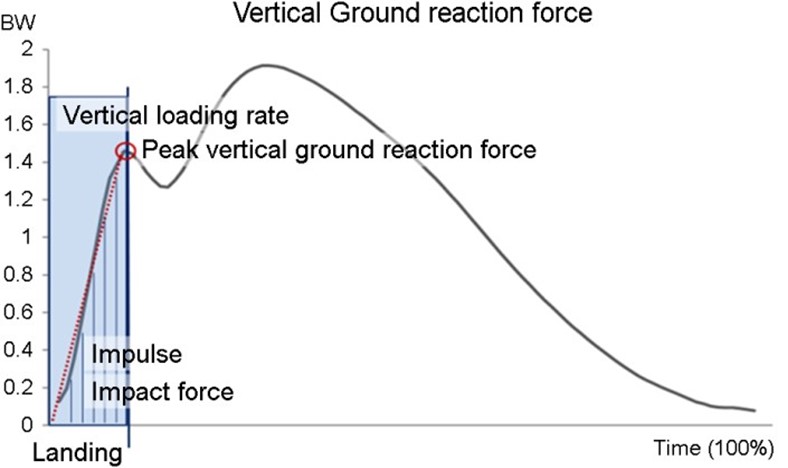
This research regarded the landing to the time when PVGRF occurred during running as the landing section and calculated the slope to the initial peak values by dividing PVGRF by time required through defining the slope as VLR delivered to the human body (Figure 4) (Ryu & Park, 2020).

The LyEs of DPA, IEA, FEA, DPAV, IEAV, and FEAV were examined without filtering raw data, and the error was regarded as constant because all participants' motions were sampled (shot) with the same equipment. The general filtering process carried out in a time-series analysis may affect the nonlinear time-series analysis, and the filtering was omitted for accurate judgment of variability within the motions (Ryu, 2006, 2007, 2008, 2009, 2014). State-space was created to judge the dynamic characteristics of running motions depending on the running shoe's properties, and existing time-series information was looked at in the state-space. The number of analysis data was 1,674 on average. The state-space was formed by adding dimension (axis) and using a time delay method (Buzzi et al., 2003; Dingwell & Cusumano, 2000; Dingwell et al., 2000; Ryu, 2006, 2007, 2008, 2009, 2014).

Here, X(t)=d means dimension state vector, x(t)=existing 2D data, T=time, delay, and d=insertion dimension. The time delay value was set to 7, and the insertion dimension was set to 5. Under the assumption that the distance between two points from the constructed state-space changes exponentially and functionally, the maximum LyE on motions was calculated as follows:

In this equation, the mean displacement between adjacent trajectories within the state-space on time, namely d(t)=time, and d0=gap between initial adjacent points. If the log is taken on both sides, LyE (λ*) is defined as follows:

Here, dj(i)=i indicates the distance between the most adjacent jth pairs after the discrete-time gap. Euclidean distance between the adjacent trajectories in the state-space was calculated as a time function and as a mean value on all the most adjacent original pairs. λ* exponents were estimated from the linear slope in line with the curve.

In this formula, < . > indicates the mean value of all j's values. The LyE of DPA, IEA, FEA, DPAV, IEAV, and FEAV is the quantified value of divergent mean exponent rate of adjacent trajectories in the state-space (Stergiou, Jensen, Bates, Scholten & Tzetzis, 2001), and it can be a measure directly evaluating sensitivity to local shaking (Kantz & Schreiber, 1997). If the exponent is a positive value, local instability is indicated, and variability means high and a lack of consistency. The motion with small variability and consistent motion indicates negative LyE or LyE converges to 0 (Buzzi et al., 2003; Dingwell & Cusumano, 2000; Dingwell et al., 2000; Ryu, 2006, 2007, 2008, 2009, 2014).

5. Statistical analysis

To compare impact variables and the dynamic stability variables of the lower extremity joint depending on the properties of running shoes, this research carried out repeated measure one-way ANOVA, the LSD method, the effect size (partial eta squared) and the statistical power was used for follow-up verification. To examine the correlations between running shoes' properties, this research looked at Pearson's correlation coefficient. The statistical processing was analyzed using the SPSS Ver. 22 software (IBM, USA), and significance level α was set to .05.

This research looked at the differences between the midsole properties (Material and method, Thickness, Dwell time, Peak acceleration and Energy return), the impact variables (PVRGF and VLR) and lower extremity joint's dynamic stability variables (LyEs of joint angle and angular velocity), among three types of running shoes with different properties during running, and the correlations between variables. The results are as follows:

1. Midsole Properties

(Table 1) shows the comparison of midsole properties between the shoes. Thickness of N, FA, and FB were 26.43±0.84 mm, 30.63±0.60 mm, and 33.38±0.17 mm, respectively. There were significant differences among the shoes, with F=482.606 (p=.032), effect size being 〖η_p〗^2=.999, statistical power being=.880, with Thickness of FB being statistically greater than N and FA (p<.05).

2. Impact Variables

(Table 2) shows the comparison of PVGRF, VLR between the shoes. PVGRFs of N, FA, and FB were 1.75±0.32 BW, 1.71±0.21 BW, and 1.88±0.26 BW, respectively. There were significant differences among the shoes, with F=12.092 (p=.000), effect size being 〖η_p〗^2=.547, statistical power being =.988, and PVGRF of FB being statistically greater than N and FA (p<.05). VLRs of N, FA, and FB were 29.49±7.57 BW/s, 28.53±5.97 BW/s, and 25.88±3.64 BW/s, respectively. There were significant differences among the shoes, as F=3.903 (p=.037). The effect size was 〖η_p〗^2=.281 and statistical power was=.635, with PVGRF of FB being statistically smaller than N and FA (p<.05).

3. LyE of Joint Angles

DPA LyEs of N, FA, and FB were 0.031±0.021, 0.039±0.021, and 0.079±0.072, respectively (Table 3). There were significant differences among the shoes, as F=3.576 (p=.047), effect size was 〖η_p〗^2=.263, and statistical power was=.595, with PVGRF of FB being statistically greater than N and FA (p<.05).

4. Correlation Coefficient

The correlation coefficient between the biomechanical impact variables and mechanical characteristics of shoes is shown in (Table 4). The dwell time positively correlated with the DPAV LyE and IEAV LyE (r=.674, r=.567). The peak acceleration positively correlated with the DPAV LyE, IEAV LyE, and FEAV LyE (r=.857, r=.731, r=.406). The energy return negatively correlated with the IEA LyE, DPAV LyE, IEAV LyE, and FEAV LyE (r=-.362, r=-.770, r=-.660, r=-.364).

This research examined the difference between the impact variables (PVRGF and VLR) and the dynamic stability variables of the lower extremity joint (LyEs of DPA, IEA, FEA, DPAV, IEAV, and FEAV) among three types of running shoes with different properties during running. This research presented correlations between variables and predicted the effects of running shoes' properties on impact and stability.

First, when looking at PVGRF and VLR directly related to the injury from running (Nigg, 2010), the PVGRF of FB was larger than the N and FA, but the VLR of FB was smaller. In research that examined correlations between the mechanical characteristics and impact absorption function of running shoes (Ha et al., 2020), PVGRF was larger, as the shoes were thicker, but VLR was smaller. In research investigating the effects of running shoes' cushioning on impact (Meardon et al., 2018), VLR was smaller since cushioning was better. As seen through the previous research, the thickest FB among the running shoes compared in this research is judged to be the most effective in impact absorption, and the first hypothesis that VLR would be smaller as running shoes became thicker was adopted.

Second, when looking at LyE that was examined in this research to evaluate the stability and consistency of repetitive running motions (Buzzi et al., 2003; Dingwell & Cusumano, 2000; Dingwell et al., 2000; Hausdorff et al., 1994; Ryu, 2006, 2007, 2008, 2009, 2014), FB's LyE of DPA was larger than that of N and FA. When examining that FB's PVGRF was the highest in a complex way, as the running shoes were thicker, it was adequate for impact absorption (i.e., small VLR), but the PVGRF at landing was large, so there was a possibility that shaking in the vertical or front and back direction increased. Therefore, FB's LyE of DPA was judged to be larger. Consequently, the second hypothesis that LyE would be larger, as running shoes became thicker, was partially adopted. Nonetheless, the correlation coefficient was not significant, so further research is required.

Third, when investigating the correlation coefficient between the mechanical characteristics and LyE of the running shoes, a positive correlation was indicated between the LyEs of DPAV, IEAV, and FEAV and the dwell time (i.e., impact absorption time) and peak acceleration, but energy return showed a negative correlation. As LyE on the angular velocity of the lower extremity joint is larger during running in that LyE can judge dynamic stability in repetitive human body motions (Buzzi et al., 2003; Dingwell & Cusumano, 2000; Dingwell et al., 2000; Hausdorff et al., 1994; Ryu, 2006, 2007, 2008, 2009, 2014), irregular or inconstant lower extremity joint motions can be judged to be revealed. Therefore, as the dwell time is longer and peak acceleration is higher in a running shoe, PVGRF at landing increases; thus, the shaking of the lower extremity joint can be caused. On the contrary, when energy return (i.e., resilience) is better, it can be said that stable and consistent motions are induced.

Based on the above result, the thick running shoes with an excellent impact absorption function are predicted to play a positive role in reducing the lower extremity joint burden for running novices or running club members. Running shoes with excellent energy return function are expected to play an effective role in the stability and consistency of elite mid- and long-distance runners or marathoners.

This research examined the effects of three types of running shoes with different properties on the impact variables (PVRGF and VLR) and the dynamic stability variables of the lower extremity joint (LyEs of DPA, IEA, FEA, DPAV, IEAV, and FEAV) during running. Although the VLR of thick running shoes (FB) was smaller than that of the other running shoes (N and FA), PVGRF and LyE of DPA were larger. Although the running shoes' dwell time (i.e., impact absorption time) and peak accel- eration positively correlated with the LyEs of DPAV, IEAV, and FEAV, the energy return showed a negative correlation. Through the above result, the thick running shoes with an excellent impact absorption function are forecast to reduce the burden of the lower extremity joint during running. The running shoes with an excellent energy return function are expected to be effective for stability and consistency during running.

In future biomechanical studies on running shoe, different results may appear between impact variables and stability (consistency) vari- ables as above, so decision of detailed analysis variables is required according to the main purpose of running shoe.