Walking can be defined as positional change of center of mass from one place to other. Human locomotion movements are basically sinusoidal oscillations or rotations which are transformed by the body into a translational movement which make it complex and to be influ- enced by so many variables (CONTINI, Gage & DRILLIS, 1965). Walking can be done in different way and the way of walking is called gait.

Stability is a critical component of gait. It can be defined as the ability to maintain functional locomotion despite the presence of small kine- matic disturbances or control errors (Goswami, Thuilot & Espiau, 1998). Position and time changes the force in the joint which makes walking charismatic. Investigation including time and position is essential for the study of balanced walking. Gait stability is being evaluated from different approach with them maximum Lyapunov exponent (MLE) gaining increasing interest during recent years. Data captured from different motion capture devices and inertial measurement units are being widely used for the calculation of MLE. MLE was first used by Dingwell, Cusumano, Sternad & Cavanagh (2000) to estimate gait stability.

In the context of gait stability, the MLE quantifies the ability of the motor system to attenuate small perturbations, which are revealed as the divergence of the trajectories in state space thus inability of the motor system to diminish the perturbations results in a higher diver- gence of the trajectories of the state space and result to greater MLE values (Mehdizadeh, 2018). The MLE thus measures the exponential rate of divergence of trajectories of the state space constructed from kinematic data acquired from gait (Dingwell & Marin, 2006). Hence, the higher value of the MLE, the lower stability of the individual’s walking. Several papers had been published regarding to the estimation of the MLE for gait but many of them have led to incongruous numerical values. This may have been due to differences in algorithm, methods of data collection and input parameters.

There are several existing algorithms to calculate MLE, some of the commonly used are Rosenstein's algorithm (Rosenstein, Collins & De Luca, 1993), Wolf's algorithm (Wolf, Swift, Swinney & Vastano, 1985) and Kantz's algorithm (Kantz, 1994). In a systematic review done by Mehdizadeh (2018), it had been found that R-algorithm was used by 79% and of the authors had used the and W-algorithm was used by 15%. The reconstruction of the phase space is the first and important step in the calculation of MLE in using any of the algorithm.

Phase space can be defined as the finite dimensional vector space that contains all the possible states of a system and each possible state corresponds to one unique point in the phase space which is used to identify the attractors in the system where attractor draws or repels nearby trajectories towards or away from itself (Baker, Baker & Gollub, 1996; Thompson & Stewart, 1986). The phase space is reconstructed using the method of time delay and embedding dimension.

Ekizos, Santuz, Schroll & Arampatzis (2018) calculated MLE by putting the markers on bony landmarks of the trunk in different walking and running trials and their finding suggests that assessment of dynamic stability using the MLE is reliable in both walking and running as MLE values obtained for running trials were significantly higher than those obtained for walking trials. Further Chakraborty & Nandy (2018) approached to dynamic stability in three different planes by MLE esti- mation of the markers positioned on different points of foot at 12 different gait speeds. Finding of their study suggest that for gait analysis should be done in three anatomical planes instead of single plain which will assist to capture the signal of human gait.

It has been observed that the range of motion of joints in anteropos- terior direction is approximately five times larger than that of vertical and mediolateral direction (Dananberg, 2000). Therefore, most of studies are done on anteriposterior direction. On the other hand, studies done by (de Morais Filho et al., 2009; Rethlefsen & Kay, 2013; Vaughan, Davis, & O'connor, 1992) suggest that calculation done on mediolateral and vertical direction also provide valuable information regarding to the stability. So, it is relevant to study in all three direction to acquire the actual information of gait signals.

The purpose of this study is to calculate and compare MLE for the anteroposterior, mediolateral and vertical displacement of the markers attached to bony land marks of trunk and foot. Further this study also aims to calculate the spatiotemporal characteristics of the subjects. This study is a small approach to understand the complex phenomenon of human gait stability.

1. Subjects

Ten young and healthy male subjects with (age, 26.5±3.27 years, body height 167.44±5.12 cm, and body mass 69.5±7.36 kg) were voluntarily participated in the study. Subjects were not suffered from any injury affecting the natural gait. Participants were trained to walk on a tread mill and were explained about the experimental procedure and aim of the study.

2. Experimental equipment

Kinematic data were collected using Opti-track motion capture system (Motive 2.1.1) with six cameras (Prime × 13). Camera calibration and ground plane setting were performed using CW-500 calibration wand kit and calibration square CS-400 respectively. Treadmill was setup in the calibrated area for the walking. Retro-reflective marker (6.4 mm) were attached to motion capture suit classic in the specific location. The suit is breathable and markers can be attached to any of the velcro-friendly surfaces for custom marker set and skeleton.

3. Experimental procedure

Preliminary phase of experiment started by introducing subject about the experiment, equipment and the way of performing. Subjects were made familiar to walk on a tread mill wearing the experimental suit. Cameras were adjusted in the designated areas such that they can capture each and every marker attached in the body of subjects. Any external noise and disturbance were removed. After that camera cali- bration was performed by repeatedly moving calibration wand kit in the capture area. Then after ground plane was set by using calibration square. Afterwards retro reflective markers were placed on different bony land marks of the body. Then the process of data capture began for which each subject walked on tread mill for five minutes with their preferred speed one after the other in the same calibration and ground plane coordinate. Then three-dimensional coordinates of different markers were recorded. Example of marker placement is shown in (Figure 1).

Figure 1. Example of marker placement.

Modify Delete

4. Data collection and analysis

Three-dimensional positional coordinate of the retro reflective marker placed on seventh cervical vertebrae (C7) Second, sixth and tenth thoracic vertebrae (T2, T6 & T10) and heel and toe of both feet were obtained after labelling and gap filling of the trajectories of markers. Smoothing feature available in the edit tools of the software (Opti-track motion capture system) was used to remove the noise in the data by applying the cut off frequency of 6 Hz. Smoothing feature applies a noise filter (low-pass butterworth, 4th degree). For the calculation of spatiotemporal characteristics of the subject position time graph of heel and toe marker were analysed. All data processing, analysing and script coding were performed in Python 3.7.

5. Statistical analysis

For the statistical analysis first of all One- way ANOVA was performed after that Tukey post hoc test was chosen to determine the significant difference in MLE values for anteroposterior, mediolateral and vertical position. Level of significance was set 0.05. Statistical analysis was done by using IBM SPSS (2019).

6. Calculation of maximum Lyapunov exponent

The reconstruction of the phase space is the first step in determining the maximum Lyapunov exponent (Kantz & Schreiber, 2004). The phase space was reconstructed using the method of delays (Broomhead & King, 1986; Takens, 1981). For an N-point time series x(n), the phase space was reconstructed using the following equation:

Where, τ being time delay and dE being embedding dimension. Thus, creating the dE-dimensional phase space as an M × dE matrix where

Time delay (τ) was calculated with the use first minimum of the AMI function. The AMI takes nonlinear correlations into account unlike the autocorrelation function. AMI evaluates the amount of information that is shared between data sets over a range of time delays (Fraser & Swinney, 1986). After wards the embedding dimension was determined using global false nearest neighbors (Kennel, Brown & Abarbanel, 1992). False nearest neighbor compares the distances between neigh- bouring trajectories at increasing dimensions. In this study τ=10 and dE= 5 was used. After wards Rostein's algorithm was used (Rosenstein et al., 1993). Nearest neighbors were located by using the Euclidean norm (denoted below as ‖ ‖), with the additional constraint that each point must be on a separate trajectory.

In order to ensure that each nearest neighbor lie on different trajec- tories, neighbors were separated for the larger time than the average duration of time series.

The mean period of the time series was calculated as the inverse of the mean power frequency. The average divergence distance of all possible nearest neighbor pairs was tracked through time creating a mean divergence curve. Least-squares fit was done to the linear slope of the divergence curve for the calculation of MLE

Where < > denotes the average over all pairs of j (nearest neighbor pairs, j = 1, 2, … , M).

Spatiotemporal characteristics of the subjects were calculated which are presented in (Table 1). Average MLE values for anteroposterior, mediolateral and vertical displacement of the markers are presented in (Table 2). The result of Tukey Post hoc test done after One-way ANOVA is presented in (Table 3). The result shows significant difference in MLE values for anteroposterior displacement with mediolateral and vertical displacement of the markers whereas MLE values for mediolateral dis- placement shows no significant difference with vertical displacement of the markers at significance level 0.05. For illustration a three-dimensional state space reconstruction of C7 marker is shown (Figure 2) and mean divergence curve of the Lorentz attractor of C7 marker is shown in (Figure 3).

Figure 2. Reconstructed state space of c7 marker

Modify Delete

Figure 3. Mean divergence curve of the Lorentz attractor of c7 marker. X-axis: Number of frames, Y-axis:

Modify Delete

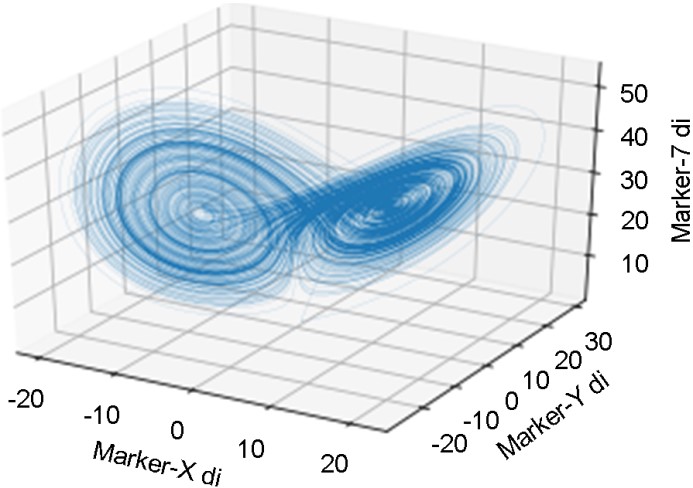
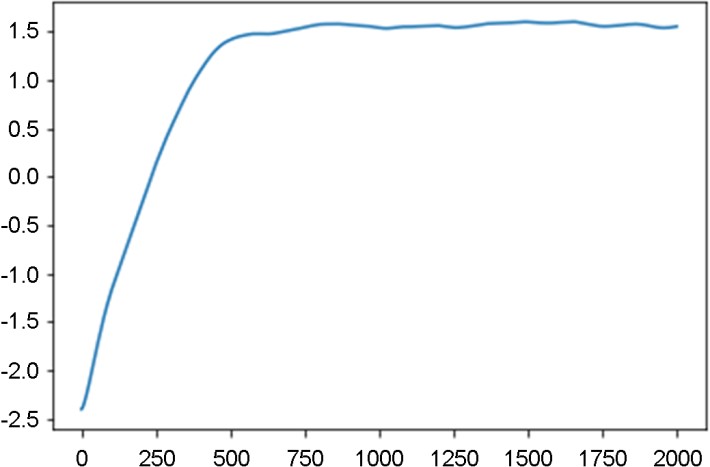
The present study aimed to calculate and compare MLE for the anteroposterior, mediolateral and vertical displacement of the marker attached on different bony land marks of the body. MLE values for the anteroposterior displacement shows significant differences with MLE values for mediolateral and vertical displacement of the markers whereas MLE values for mediolateral displacement shows no significant difference with MLE values vertical displacement of the marker. Further this study also calculated the different spatiotemporal gait characteristics of the subject.

In this study the preferred walking speed of the subjects is (1.32±0.14) which is in agreement with the study (Mohler, Thompson, Creem-Regehr, Pick & Warren, 2007). Other calculated spatiotemporal char- acteristics of the subject are congenial with the study (Park & Kim, 2004). In this study subjects walked in tread mill as it allows ambulation within small area and facilitates the use of static camera and moni- toring equipment (Alton, Baldey, Caplan & Morrissey, 1998; Riley, Paolini, Della Croce, Paylo & Kerrigan, 2007).

In this study markers attached to bony land marks of the trunk and foot were studied separately. Trunk plays prominent role in the postural control in order to allow successful execution of functional activities as the gait (Leteneur, Gillet, Sadeghi, Allard & Barbier, 2009). Foot plays great role in the different stages of gait cycle (Roberts, 2010). Moreover out of seven cervical vertebrae we studied about only C7 as C7 plays sensitive role in head balancing and head stability is the crucial com- ponent of locomotion (Nalley & Grider-Potter, 2019).

36,000 frames were recorded in 300 seconds to acquire adequate numbers of strides. Kinematic data in this study were filter by applying cut off frequency of 6 HZ. Regarding to data filtering for the calcula- tion of MLE, study done by Raffalt, Senderling & Stergiou (2020) and Mehdizadeh & Sanjari (2017) have different conclusion however we filter the data after the complete labelling of the markers for removing the unnecessary noises.

MLE values calculated in this study are in agreement with those calculated by Smith (2019) with respect to time delay, embedding dimension and number of nearest neighbour (Buzzi, Stergiou, Kurz, Hageman & Heidel, 2003; Kang & Dingwell, 2008; Mehdizadeh, 2018; Terrier & Reynard, 2015) compare between young and older subjects to investigate gait stability using MLE. The finding of these studies for young subjects has similarities with the finding of this study. The lower MLE values obtained in this study symbolize the stable gait of the subjects. MLE values obtained in the study (Park & Kim, 2004) for the vertical displacement of the ankle were less for healthy subjects then for unhealthy subjects which symbolize instability of unhealthy subjects.

In the study (Ryu, 2019), different mle values were obtained for the different directional movent of knee, ankle and hip joint. Obtained values were dissimilar for the faller and not faller group. The result in the above study and this study also supports for the consideration of all three direction while calculating MLE for accessing the stability.

Previous studies had inconsistent finding regarding on which signal direction AP, ML or VT characterizes the largest differences in MLE. van Schooten et al. (2015) reported difference all direction while (Lockhart & Liu, 2008) found difference only in VT whereas (Bizovska, Svoboda, Janura, Bisi & Vuillerme, 2018; Huijben, Van Schooten, Van Dieën & Pijnappels, 2018) found difference in ML and (Howcroft, Kofman, Lemaire & McIlroy, 2016) found difference in AP. In the above studies data were collected using inertial sensors and accelerometers and acceleration was used for the calculation of MLE whereas this study used motion capture system and velocity obtained from the position coordinate was used for the calculation of MLE.

MLE is being used in different areas and among different population groups for studying gait stability but not all of these studies are com- parable. Use of MLE in sports biomechanics can be of greater import- ance as it access stability. It can be used in the selection procedure of the athletes for Paralympic games. Further it can be used to test the effect of training program for the balance on the gait stability.

This study calculates and compare the maximum Lyapunov exponent for the anteroposterior, mediolateral and vertical displacement of the markers attached to different bony land marks of the body. Calculated MLE values indicates the stable gait of young and healthy subject. Comparison shows the significant difference in MLE values for different displacement. Results of this study suggest that it is essential to con- sider the displacement of markers in three direction to examine the real characteristic of a gait signal.